Category Archives: PROLOG

機械の買い替え問題（Renewal Plan Problem)を解くプログラム

ECLiPSe CLPで機械の買い換え問題（Problems and exercises in Operations Researchの1.5 Renewal plan）を解くプログラムの説明をします。

問題：
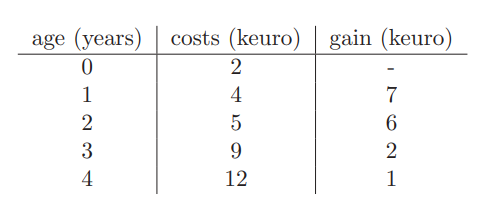
ある会社が12000ユーロの機械を購入し使用しています。機械には毎年維持費(costs)がかかります（維持費は年々上がっていきます）。
使用中の機械は中古で販売(gain)し新しく買いなおすこともできます（中古機械の販売価格は年々下がっていきます）
維持費と中古機械の販売価格は以下の表のとおりになっています（1keuroは1000ユーロ）。
5年間の総運用コストを最小限に抑える機械の買い換え計画を決定しなさい。

行間を読むとこの問題は機械の生産する利益に関しては触れられていないのでこれは毎年一定で考慮する必要なしということのようです。

難しくて解けなかったので答えと解説を見ました。説明します。
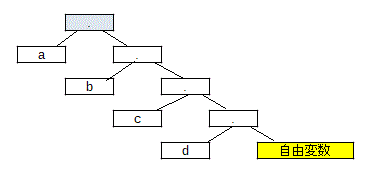
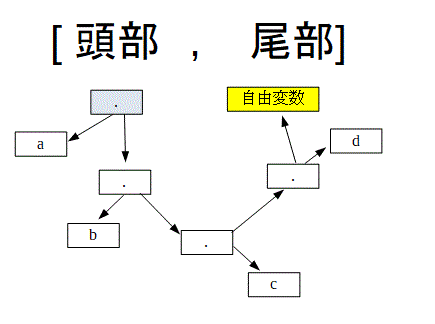
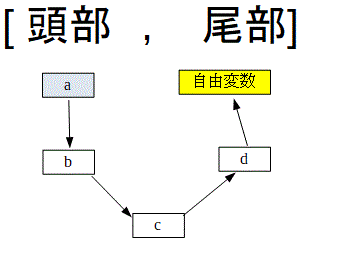
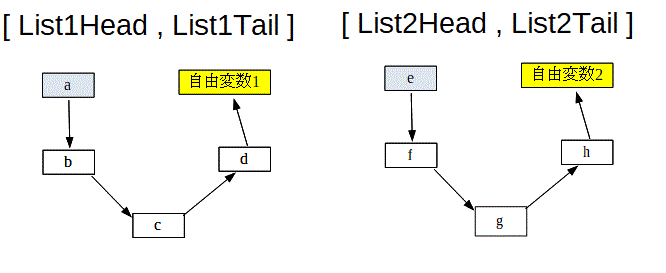
「i年目に購入した機械をj年目まで使用し、買い替えたときのコスト」をCijという変数で表し、1～6年目時点を表す6つのノードがCijで結ばれた有向グラフを考える（6は5年間の期限終了時を表す）
Cijの計算方法は以下となります。

Cij = 12000 + [(j-i)年間にかかった維持費] – [(j-i)年使用した機械の中古販売価格]

たとえば　2年目に購入した機械を4年目まで使用し買い替えたコストだと
C24 = 12000 + (2000+4000) – 6000 = 12000
となります。これはノード2とノード4を結ぶエッジとなります。
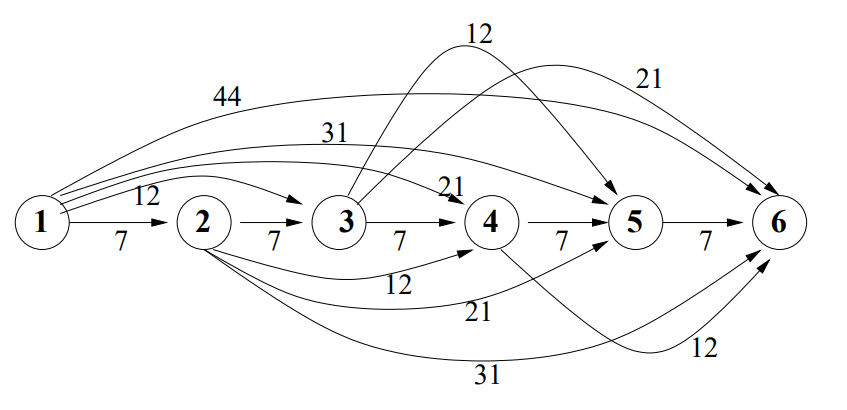
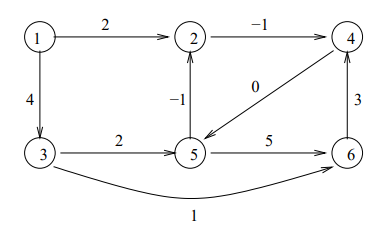
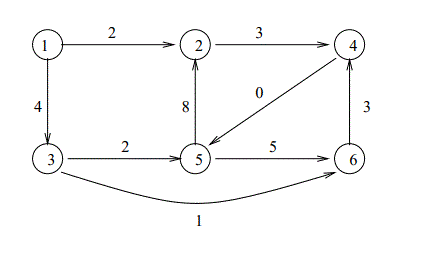
そのように計算した有向グラフは以下のようになります（回答からコピー）

このようなグラフの、ノード１からノード６へ至る最小コストの経路が答えとなります。

single_pair_short_path/6を使用すると、最小コストの経路をすべて取得できます。

single_pair_short_path(+Graph, +DistanceArg, +SourceNode, +SinkNode, +Tolerance, -Path)
　+Tolerance を 0にするとすべての最小コストの経路が取得され、当然それらのコストはみな同じとなります。
　+Tolerance に0より大きい数値を設定すると、最小＋その値　までのコストの経路も抽出されるようです。

プログラム

:-lib(graph_algorithms).

solve(Path):-
	make_graph(6,
		[ 
			e(1,2,7),
			e(1,3,12),
			e(1,4,21),
			e(1,5,31),
			e(1,6,44),
			e(2,3,7),
			e(2,4,12),
			e(2,5,21),
			e(2,6,31),
			e(3,4,7),
			e(3,5,12),
			e(3,6,21),
			e(4,5,7),
			e(4,6,12),
			e(5,6,7)
		],Graph),
	single_pair_short_path(Graph, 0, 1, 6, 0, Path).

:-lib(graph_algorithms).

solve(Path):-

make_graph(6,

[

e(1,2,7),

e(1,3,12),

e(1,4,21),

e(1,5,31),

e(1,6,44),

e(2,3,7),

e(2,4,12),

e(2,5,21),

e(2,6,31),

e(3,4,7),

e(3,5,12),

e(3,6,21),

e(4,5,7),

e(4,6,12),

e(5,6,7)

],Graph),

single_pair_short_path(Graph, 0, 1, 6, 0, Path).

実行結果：

?- solve(Path).
Path = 31 - [e(5, 6, 7), e(3, 5, 12), e(1, 3, 12)]
Yes (0.00s cpu, solution 1, maybe more)
Path = 31 - [e(4, 6, 12), e(3, 4, 7), e(1, 3, 12)]
Yes (0.00s cpu, solution 2, maybe more)
Path = 31 - [e(4, 6, 12), e(2, 4, 12), e(1, 2, 7)]
Yes (0.00s cpu, solution 3)

?- solve(Path).

Path = 31 - [e(5, 6, 7), e(3, 5, 12), e(1, 3, 12)]

Yes (0.00s cpu, solution 1, maybe more)

Path = 31 - [e(4, 6, 12), e(3, 4, 7), e(1, 3, 12)]

Yes (0.00s cpu, solution 2, maybe more)

Path = 31 - [e(4, 6, 12), e(2, 4, 12), e(1, 2, 7)]

Yes (0.00s cpu, solution 3)

コストは31(=31000ユーロ)が最小で、以下の買い換え計画があるようです。
3年目と5年目で買い替える
3年目と4年目で買い替える
2年目と4年目で買い替える

グラフの最小カット(the Minimum Cut)を求める

Leave a reply

ECLiPSe CLPでグラフの最小カットを求める方法を説明します。

グラフのカットというのは、最大流問題で用いた、エッジに許容流量の設定のあるスタートとゴールのノードを持つ有向グラフのすべてのノードを、「スタート側」「ゴール側」の2種類のノードに分けることをいいます。

ノードをどのように分けてもよいので、カットの仕方には複数通りの方法があります。
グラフに|V|個のノードがあったとして、スタートとゴールのノードのみどちら側か決まっているので　2^(|V|-2)通り　のカットの方法があります。

最小カットというのは、複数あるカットのうち、「カット容量が最小となるもの(そしてその容量)」のことを言います。
カット容量とは、ノードとノードを結ぶすべてのエッジのうち「スタート側に属するノード」から「ゴール側に属するノード」の方向のエッジの許容流量の総計のことを言います（スタート側→スタート側、ゴール側→ゴール側、ゴール側→スタート側のエッジの容量は数えない）

最小カット容量は、スタート→ゴールの流れのボトルネックのようなもので、この値がそのまま最大流と等しくなるとのことです。
（最小カット容量＝最大フロー）

前置き長くなりましたが上記最小カットを求めます。
library(all_min_cuts) の述語 all_min_cuts/8 を使います。

all_min_cuts(+Graph, +CapacityArg, +SourceNode, +SinkNode, -MaxFlowValue, -MaxFlowEdges, -MinCuts, -MinCutEdges)

Grapha – グラフ
CapacityArg – エッジ e(_,_,A) のAのどこが最大流量か設定する
SourceNode – スタートのノード番号
SinkNode – ゴールのノード番号
MaxFlowValue – 最大フロー(=最小カット容量)(戻り値)
MaxFlowEdges – 「フロー　- エッジ」のリスト(戻り値)
MinCuts – 最小カット容量をもつカットのリスト（複数あれば複数）(戻り値)
MinCutEdges – すべての最小カット組（それぞれのカット組はスタート側-ゴール側を分けるエッジのリスト）(戻り値)

①以下の図でノード１がスタート、ノード7がゴールとして最小カットを求めます。

プログラム：

:-lib(graph_algorithms).
:-lib(all_min_cuts).

solve(MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges):-
	make_graph(
		7,
		[ 
			e(1,2,6),
			e(1,3,6),
			e(2,3,1),
			e(2,4,3),
			e(2,5,3),
			e(3,5,7),
			e(4,5,1),
			e(4,7,1),
			e(5,7,4),
			e(5,6,5),
			e(6,7,4)
		],
		Graph),
	all_min_cuts(Graph, 0, 1, 7, MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges).

:-lib(graph_algorithms).

:-lib(all_min_cuts).

solve(MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges):-

make_graph(

[

e(1,2,6),

e(1,3,6),

e(2,3,1),

e(2,4,3),

e(2,5,3),

e(3,5,7),

e(4,5,1),

e(4,7,1),

e(5,7,4),

e(5,6,5),

e(6,7,4)

Graph),

all_min_cuts(Graph, 0, 1, 7, MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges).

実行結果（見やすいように手で改行入れてます）：

?- solve(MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges).
MaxFlowValue = 9
MaxFlowEdges = 
[
4 - e(6, 7, 4), 
4 - e(5, 7, 4), 
4 - e(5, 6, 5), 
1 - e(4, 7, 1), 
1 - e(4, 5, 1), 
4 - e(3, 5, 7), 
3 - e(2, 5, 3), 
2 - e(2, 4, 3), 
4 - e(1, 3, 6), 
5 - e(1, 2, 6)
]
MinCuts = [[2, 5, 3, 6, 1, 4]]
MinCutEdges = 
[
[
e(4, 7, 1), 
e(6, 7, 4), 
e(5, 7, 4)
]
]
Yes (0.00s cpu)

?- solve(MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges).

MaxFlowValue = 9

MaxFlowEdges =

[

4 - e(6, 7, 4),

4 - e(5, 7, 4),

4 - e(5, 6, 5),

1 - e(4, 7, 1),

1 - e(4, 5, 1),

4 - e(3, 5, 7),

3 - e(2, 5, 3),

2 - e(2, 4, 3),

4 - e(1, 3, 6),

5 - e(1, 2, 6)

]

MinCuts = [[2, 5, 3, 6, 1, 4]]

MinCutEdges =

[

e(4, 7, 1),

e(6, 7, 4),

e(5, 7, 4)

]

Yes (0.00s cpu)

最小カットは９で
ノード　4-7、6-7、5-7　のエッジがスタート側とゴール側を分けるエッジのようです。

②以下のグラフで最小カットを求めます。

プログラム（便宜的にスタートノードとゴールノードをそれぞれノード5、ノード6に置き換え）：

:-lib(graph_algorithms).
:-lib(all_min_cuts).

solve(MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges):-
	make_graph(
		6,
		[ 
			e(5,1,3),
			e(5,2,10),
			e(1,4,4),
			e(1,3,4),
			e(2,1,7),
			e(2,3,2),
			e(4,2,3),
			e(4,3,8),
			e(4,6,3),
			e(3,6,8)
		],
		Graph),
	all_min_cuts(Graph, 0, 5, 6, MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges).

:-lib(graph_algorithms).

:-lib(all_min_cuts).

solve(MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges):-

make_graph(

[

e(5,1,3),

e(5,2,10),

e(1,4,4),

e(1,3,4),

e(2,1,7),

e(2,3,2),

e(4,2,3),

e(4,3,8),

e(4,6,3),

e(3,6,8)

Graph),

all_min_cuts(Graph, 0, 5, 6, MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges).

実行結果：

?- solve(MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges).
MaxFlowValue = 10
MaxFlowEdges = 
[
	7 - e(5, 2, 10), 
	3 - e(5, 1, 3), 
	3 - e(4, 6, 3), 
	1 - e(4, 3, 8), 
	7 - e(3, 6, 8), 
	2 - e(2, 3, 2), 
	5 - e(2, 1, 7), 
	4 - e(1, 4, 4), 
	4 - e(1, 3, 4)
]
MinCuts = [[2, 5, 1]]
MinCutEdges = 
[
	[e(1, 4, 4), e(1, 3, 4), e(2, 3, 2)]
]
Yes (0.02s cpu)

?- solve(MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges).

MaxFlowValue = 10

MaxFlowEdges =

[

7 - e(5, 2, 10),

3 - e(5, 1, 3),

3 - e(4, 6, 3),

1 - e(4, 3, 8),

7 - e(3, 6, 8),

2 - e(2, 3, 2),

5 - e(2, 1, 7),

4 - e(1, 4, 4),

4 - e(1, 3, 4)

]

MinCuts = [[2, 5, 1]]

MinCutEdges =

[

[e(1, 4, 4), e(1, 3, 4), e(2, 3, 2)]

]

Yes (0.02s cpu)

最大フロー(最小カット)10、
ノード1-4、1-3、2-3　を結ぶエッジがスタート側とゴール側を結ぶ

最大流問題(Maximum flow Problem)を解く

Leave a reply

ECLiPSe CLPで最大流問題を解く方法の説明をします。
最大流問題って自分は知らなかったのですが、グラフが与えられ、ノードからノードを結ぶそれぞれのエッジに転送量の上限（転送するのはデータでも物でも何でも良い）が決められているとき、あるノードからもう一つのノードへの最大の転送量を求めるという問題です。

電子回路のキルヒホッフの法則のように、各ノードに入る量とそのノードから出ていく量は一致している必要があります（始点と終点は除く）つまりあるノードに注目したとき、入ってくる量の許容量が6で出ていく量の許容量が4の場合は少ない方の4に合わされてしまうことになります（ボトルネックとなる）

自分の勝手な解釈ですが、いくつかのノードが接続された形の水道管ネットワークみたいのがあったとして、ノード同士をつなぐ水道管の最大流量が決まっているとき、入口Aから出口Bに流せる最大の水の量を求めるみたいな感じかなとイメージしました。

以下のようなグラフ（Problems and exercises in Operations Research 10ページ目 1.3 Maximum flow の図）が与えられたときにノード1からノード7への最大流を求めるプログラムを書きます。
エッジの数値はノード間の距離ではなくエッジの許容流量を表していることに注意です。

library(max_flow)を使用します。
またlibrary(graph_algorithms)も使用します。

グラフの作成はmake_graph/3を使用します（使い方は以前の記事参照）

最大流問題を解く述語はmax_flow/5やmax_flow/7ですが、今回は得られる情報が多いmax_flow/7を使用します。

max_flow(
　　+Graph,
　　+CapacityArg,
　　+SourceNode,
　　+SinkNode,
　　-MaxFlowValue,
　　-MaxFlowEdges,
　　-MaxFlowEdgesGraph)

引数の意味は以下となります。
　1.Graph　生成したグラフ
　2.CapacityArg エッジの許容量をどこに書いたか指定
　　（e(_,_,Capacity)のCapacityの部分に数値で記載した場合は0)
　3.SourceNode 開始ノード番号
　4.SinkNode 終了ノード番号
　5.MaxFlowValue 最大流量（戻り値）
　6.MaxFlowEdges 使用されたエッジとそのエッジに流される流量
　　（流量ゼロのエッジは出力されない）　（戻り値）
　7.MaxFlowEdgesGraph 使用されたエッジをグラフの形で出力
　　（流量ゼロのエッジは出力されない）　（戻り値）

プログラム：

:-lib(graph_algorithms).
:-lib(max_flow).

solve(MaxFlowValue,MaxFlowEdges,MaxFlowEdgesGraph):-
	make_graph(
		7,
		[ 
			e(1,2,6),
			e(1,3,6),
			e(2,3,1),
			e(2,4,3),
			e(2,5,3),
			e(3,5,7),
			e(4,5,1),
			e(4,7,1),
			e(5,7,4),
			e(5,6,5),
			e(6,7,4)
		],
		Graph),
	max_flow(Graph, 0, 1, 7, MaxFlowValue,MaxFlowEdges,MaxFlowEdgesGraph).

:-lib(graph_algorithms).

:-lib(max_flow).

solve(MaxFlowValue,MaxFlowEdges,MaxFlowEdgesGraph):-

make_graph(

[

e(1,2,6),

e(1,3,6),

e(2,3,1),

e(2,4,3),

e(2,5,3),

e(3,5,7),

e(4,5,1),

e(4,7,1),

e(5,7,4),

e(5,6,5),

e(6,7,4)

Graph),

max_flow(Graph, 0, 1, 7, MaxFlowValue,MaxFlowEdges,MaxFlowEdgesGraph).

実行結果（見やすくなるよう手で改行入れてます）：

?- solve(MaxFlow, Edges, Graph).
MaxFlow = 9
Edges = 
[
4 - e(6, 7, 4), 
4 - e(5, 7, 4), 
4 - e(5, 6, 5), 
1 - e(4, 7, 1), 
1 - e(4, 5, 1), 
4 - e(3, 5, 7), 
3 - e(2, 5, 3), 
2 - e(2, 4, 3), 
4 - e(1, 3, 6), 
5 - e(1, 2, 6)
]
Graph = 
graph(7, 
[](
[e(1, 2, 6), e(1, 3, 6)], 
[e(2, 4, 3), e(2, 5, 3)], 
[e(3, 5, 7)], 
[e(4, 5, 1), e(4, 7, 1)], 
[e(5, 6, 5), e(5, 7, 4)], 
[e(6, 7, 4)], []),
 _2193, _2194, _2195, _2196, _2197, _2198)
Yes (0.00s cpu)

?- solve(MaxFlow, Edges, Graph).

MaxFlow = 9

Edges =

[

4 - e(6, 7, 4),

4 - e(5, 7, 4),

4 - e(5, 6, 5),

1 - e(4, 7, 1),

1 - e(4, 5, 1),

4 - e(3, 5, 7),

3 - e(2, 5, 3),

2 - e(2, 4, 3),

4 - e(1, 3, 6),

5 - e(1, 2, 6)

]

Graph =

graph(7,

[](

[e(1, 2, 6), e(1, 3, 6)],

[e(2, 4, 3), e(2, 5, 3)],

[e(3, 5, 7)],

[e(4, 5, 1), e(4, 7, 1)],

[e(5, 6, 5), e(5, 7, 4)],

[e(6, 7, 4)], []),

_2193, _2194, _2195, _2196, _2197, _2198)

Yes (0.00s cpu)

最大9の量流せるようですね。

一応注意点ですがこのlibrary(max_flow)はステータスが「prototype」となっていることに気を付けてください。もしバグ見つかったらECLiPSeの開発者に報告すると喜ばれます。手間でしたら私（koyahataアットマークkoyahatataku.com)に報告くだされば私が報告します。

以上

Bellman-Ford’sアルゴリズムを用いてグラフの最短経路木(shortest path tree)を求める

Leave a reply

ECLiPSe CLPを使ってグラフの最短経路木(shortest path tree)を求める方法を説明します。

前回の例ではshortest_paths/4を使用して最短経路木を求めましたが、今回はshortest_paths_bellman_ford/4を使用しBellman-Ford’sアルゴリズムで求めます。

特徴としては、前回の例ではコストは負の数が許されなかったのですが、Bellman-Ford’sアルゴリズムでは負のコストも許されます。マニュアルには記載されていませんが前回のshortest_paths/4はおそらくダイクストラ法を使っているのではと予想しています（ソースにもコメントなし）。

以下のようなグラフ（Problems and exercises in Operations Research 9ページ目 1.2 Bellman-Ford’s algorithm の図）で最短経路木を求めます。

shortest_paths_bellman_ford/4 の引数はコストに負数が許されること以外はshortest_paths/4と同じなので説明を割愛します（前回記事を参照）

プログラム：

:-lib(graph_algorithms).

solve(Path):-
	make_graph(
		6,
		[ 
			e(1,2,2),
			e(2,4,-1),
			e(1,3,4),
			e(3,5,2),
			e(5,2,-1),
			e(5,6,5),
			e(4,5,0),
			e(6,4,3),
			e(3,6,1)
		],
		Graph),
	shortest_paths(Graph,0,1,Path).

:-lib(graph_algorithms).

solve(Path):-

make_graph(

[

e(1,2,2),

e(2,4,-1),

e(1,3,4),

e(3,5,2),

e(5,2,-1),

e(5,6,5),

e(4,5,0),

e(6,4,3),

e(3,6,1)

Graph),

shortest_paths(Graph,0,1,Path).

実行結果（見やすくするために改行を手で入れてます）：

?- solve(Path).
Path = 
[](0 - [], 
2 - [e(1, 2, 2)], 
4 - [e(1, 3, 4)], 
1 - [e(2, 4, -1), e(1, 2, 2)], 
1 - [e(4, 5, 0), e(2, 4, -1), e(1, 2, 2)], 
5 - [e(3, 6, 1), e(1, 3, 4)])
Yes (0.00s cpu)

?- solve(Path).

Path =

[](0 - [],

2 - [e(1, 2, 2)],

4 - [e(1, 3, 4)],

1 - [e(2, 4, -1), e(1, 2, 2)],

1 - [e(4, 5, 0), e(2, 4, -1), e(1, 2, 2)],

5 - [e(3, 6, 1), e(1, 3, 4)])

Yes (0.00s cpu)

出力結果の見方は前回記事と同じ

総コストが負となるループがある場合（この例ではノード2->4->5) 何度もそのループを回ることでいくらでもコストを下げられるので「一番コストが低い経路」というのは存在しないのですが、ここらへんの説明はドキュメントにはありませんでした。常識的に考えるとノードを重複して通らない前提で一番コストが低い経路を返しているとは思いますが…

本記事で説明した「あるスタート地点からすべてのノードへの経路（1対N）」ではなく「あるスタート地点からあるゴールまでの経路（1対1）」を求めるsingle_pair_という接頭語が付いた述語もありますので興味のある方は調べてみてください。

グラフの最短経路木(shortest path tree)を求める

Leave a reply

ECLiPSe CLPでグラフの最短経路木を求めるやり方の紹介をします。

graph_algorithmsライブラリが使用できます。

まずmake_graph/3でグラフを作成します。引数の意味は、
第一引数：ノードの個数
第二引数：エッジ群の情報
第三引数：生成されたグラフ（戻り値）

例えば以下のグラフ（Problems and exercises in Operations Research 9ページ目 1.1 Dijkstra’s algorithm の図）の場合：

	make_graph(
		6,
		[ 
			e(1,2,2),
			e(2,4,3),
			e(1,3,4),
			e(3,5,2),
			e(5,2,8),
			e(5,6,5),
			e(4,5,0),
			e(6,4,3),
			e(3,6,1)
		],
		Graph)

make_graph(

[

e(1,2,2),

e(2,4,3),

e(1,3,4),

e(3,5,2),

e(5,2,8),

e(5,6,5),

e(4,5,0),

e(6,4,3),

e(3,6,1)

Graph)

みたいな感じで定義します。e のとこの意味は
e(ノード１番号,ノード２番号,コスト）
みたいな感じです（ノード１→ノード２の向きが存在します）
このコストのところはもっと複雑な情報を設定できるようです。
無向グラフの場合は逆向きエッジの定義も必要となります。

最短経路木なのですが、shortest_paths/4を使用して得ることが出来ます。
引数の意味は
第一引数：先ほど作ったグラフ
第二引数：e(_,_,EdgeData)で定義したエッジの3番目の引数EdgeDataのどの引数を距離（コスト）として使用するか（今回は0)
第三引数：スタート地点のノード番号
第四引数：生成された経路情報

第二引数の説明は以下を読んでください
DistanceArg refers to the graph's EdgeData information that was specified when the graph was constructed. If EdgeData is a simple number, then DistanceArg should be 0 and EdgeData will be taken as the length of the edge. If EdgeData is a compound data structure, DistanceArg should be a number between 1 and the arity of that structure and determines which argument of the EdgeData structure will be interpreted as the edge's length. Important: the distance information in EdgeData must be a non-negative number, and the numeric type (integer, float, etc) must be the same in all edges.

If DistanceArg is given as -1, then any EdgeData is ignored and the length of every edge is assumed to be equal to 1.
意訳：
DistanceArgには
・e(_,_,EdgeData)のEdgeDataが1つの数値で表されている場合は0を指定
・すべてのエッジの距離が1固定の場合は-1を指定
・「1～EdgeDataのアリティ」の範囲内で指定した場合は復号項(compound term)の何番目に距離が設定されてるかを指定したことになる
距離（コスト）は非負の数値のみ許可される。

今回の定義でノード１からすべてのノードへの最短経路を取得する場合は、以下のように呼びます

shortest_paths(Graph,0,1,Path)

1	shortest_paths(Graph,0,1,Path)

プログラム全体と結果は以下のようになります。

プログラム：

:-lib(graph_algorithms).

solve(Path):-
	make_graph(
		6,
		[ 
			e(1,2,2),
			e(2,4,3),
			e(1,3,4),
			e(3,5,2),
			e(5,2,8),
			e(5,6,5),
			e(4,5,0),
			e(6,4,3),
			e(3,6,1)
		],
		Graph),
	shortest_paths(Graph,0,1,Path).

:-lib(graph_algorithms).

solve(Path):-

make_graph(

[

e(1,2,2),

e(2,4,3),

e(1,3,4),

e(3,5,2),

e(5,2,8),

e(5,6,5),

e(4,5,0),

e(6,4,3),

e(3,6,1)

Graph),

shortest_paths(Graph,0,1,Path).

結果（見づらいのでPathのとこ改行しました。本当は1行でダダっと出ます）：

?- solve(Path).
Path = 
[](
0 - [], 
2 - [e(1, 2, 2)], 
4 - [e(1, 3, 4)], 
5 - [e(2, 4, 3), e(1, 2, 2)], 
5 - [e(4, 5, 0), e(2, 4, 3), e(1, 2, 2)], 
5 - [e(3, 6, 1), e(1, 3, 4)]
)
Yes (0.00s cpu)

?- solve(Path).

Path =

[](

0 - [],

2 - [e(1, 2, 2)],

4 - [e(1, 3, 4)],

5 - [e(2, 4, 3), e(1, 2, 2)],

5 - [e(4, 5, 0), e(2, 4, 3), e(1, 2, 2)],

5 - [e(3, 6, 1), e(1, 3, 4)]

)

Yes (0.00s cpu)

結果のPathの見方なのですが、
最初の 0 – [] （おそらく自分自身へ行く経路）のあと、
ノード2へ行く最短パス、ノード3へ行く最短パス、、、ノード6へ行く最短パス
がそれぞれ表示されてます。
2 – [～]、4 – [～]の初めの数字はかかるコストが出てます。
続くリストは、どのエッジを通ったかをリストアップしてるのですが、目的地（ゴール）～ノード１（スタート）の順で出てます

以上

[Debian]LinuxでECLiPSe CLPをビルドする

Leave a reply

LinuxでECLiPSe CLPをビルドする手順を書きます。

何でビルドするかというと、先日ECLiPSeのメイン開発者の Joachim Schimpf さんに「ECLiPSeのContributorになりたい」というメールを送ったら、「ビルド・インストール関連の作業でできることがたくさんあり、例えばDebian packageなど出来ればよい（今は./RUNMEという独自シェルスクリプトでインストールする）」と言われたので、その作業の一環としてやってます。ビルドのやり方を記事にまとめるのも立派なContribute作業だと思いますので以下に手順記載します。

ちなみにただインストールするだけならばずっと簡単な手順があり、そのうち紹介します。

ディストリビューション:Debian バージョン10.9
ECLiPSe CLPのバージョン:7.0_54
目標：ダウンロードしたソースから、root以外の全ユーザーがtkeclipseコマンドでtkeclipse起動・eclipseコマンドでeclipse起動できる状態までもっていく
この作業でできないこと：
COIN-ORのインストール
CPLEXのインストール
XPRESS-MPのインストール
JAVAインターフェースのインストール
GraphVizのインストール
FlexLMのインストール
MySQLインターフェースのインストール

ディレクトリ構成やアーキテクチャ(以下の例では64bit)など、適宜自分の環境に読み替えてください。また、ソースをビルド・インストールする際はソースディレクトリのINSTALLファイルなど目を通しておいてください。

以下はDebianをインストールした直後からの手順です。基本rootで作業してます。

ECLiPSeダウンロードページ
/usr/local/srcに移動し、wgetでECLiPSeのソースを取得し、解凍する

build essential をインストールする

mkdir /vol/Eclipse/thirdparty を作成し、ECLiPSeのサーバからtcltk.tgzを取得・解凍する（最新の8.6のライブラリだとコンパイルエラーとなるのでここで手に入る8.5を使用します）

ディレクトリの名称をtcl8.5に変更します

m4をインストールします(次のGMPのビルドで必要となる）

GMPのソースを取得、解凍します。lzファイルの解凍のためにlzipインストールします。

gmpのフォルダに入り./configureを実行

makeを実行

make checkを実行

make instalを実行

はじめにダウンロードしたEclipseのソースのフォルダに移動します。
ECLIPSEARCH=x86_64_linux
ECLIPSETHIRDPARTY=/vol/Eclipse/thirdparty
を設定したのち、./configureを実行（詳しくは同じフォルダのINSTALLというファイル見てください）

make -f Makefile.$ECLIPSEARCH を実行

./RUNMEを実行

Enter押下

インストール先は/usr/local/binにしました。

Enter

tcl/tk用のパス設定を行います。多分このままで良いのですが、一応配置した/vol/Eclipse/thirdpartyに変更しました。

不要となった圧縮ファイルを削除します。

exitで一般ユーザーに戻り「tkeclipse」コマンドでtkeclipseが、「eclipse」コマンドでeclipseが起動するようになりました。

ECLiPSe の Nonogram Solver の解説

Leave a reply

ECLiPSe CLPのexampleページにあるnonogram solverを解析していて、大体理解したので説明します。（内部で regular expression constraintを使用しています。）
nonogramは日本でいうところのお絵かきロジック、ピクロスです。

ルールの説明は割愛します。

プログラムの説明も細かいところ端折ってエッセンスの説明だけします。
このプログラムの一番重要な部分は、それぞれの行列のヒントのリスト(例えば[3,3,2]など)から盤面を表すリストの制約を生成するline述語で、この内容がわかれば8割方理解したことになります。

line述語にはヒントのリストと盤面1行分(or1列分)のリストを渡します。
line述語内でfromtoを駆使してヒントからTableに怪しげなリストを生成しています。

以下の例では、tkeclipseのコンソール？で
length(Xs,15),line([3,2,3],Xs).
と入力してステップ実行した結果です。これは、ピクロスの問題でいうところの、ヒントとして「3,2,3」が与えられた15マスの1つの行の制約をつける処理に相当します。

このfromtoの説明も今回は割愛します。このプログラムではあまり良い使い方してないので他の例で学んだほうが良いです。fromtoなどのLogical Loopはかなり重要なのでいつか改めて解説記事書くと思います。

このTableなのですが、fromtoの操作が終了した時点では図のような内容になっています（右の四角内）

並べ替えて書くと以下の内容です（ここら辺ぐちゃぐちゃに登録してるのがこのプログラムの良くない≒テキトーなところなので見習わなくて良いです）
[0,1,1]
[1,1,2]
[1,2,3]
[1,3,4]
[0,4,5]
[0,5,5]
[1,5,6]
[1,6,7]
[0,7,8]
[0,8,8]
[1,8,9]
[1,9,10]
[1,10,11]
[0,11,11]

このリストなのですが、オートマトンの状態遷移表を意味していて、盤面のリストを左から読み込んでいった際の状態の変遷を記述してます。
3つある数字の意味は
[読み込んだ数字(0 or 1), 現在の状態, 次の状態]
を表していて、
「現在の状態　で　0または1　を読み込んだら　次はどの状態になるか」
をすべて書き出しています。

状態を11個持つ以下のようなオートマトンが出来たことになります。便宜的に状態にqをつけました。

状態はq1から開始し、矢印に書いてある数字を読み込んだ際に次の状態に遷移します。
矢印がない数字が入力された際はヒントの条件を破ってしまっているのでオートマトン不受理（エラー、制約違反）となります。
q11の状態が最終状態（受理≒読み込み終わったときにこの状態であればOK）となります。

状態遷移表が完成したのち、それをregularという術語に渡して実際の制約を作成しています。

regularの説明です。
Qsは状態のリストです。この例では15個数字を読み込むので、それぞれの読み込み時に対応したものとなります。作成したオートマトンから、上記の例だと最初の状態がq1、最後Qnがq11となります。
与えられた盤面の1行(列)のリストに「現在の状態」「次の状態」の2つの変数を追加して
[マス目の数字, 現在の状態, 次の状態]
が1要素となるリスト（この例だと要素は15個）を作成しています。
状態の部分にはQsの要素を順番に指定して以下のように隣の要素同士を関連付けています。

そして、それぞれの要素に関し
(Goal infers ac)@Module

で実際の制約をつけるのですが、これが実際どのようにコールされているかというと、
member([マス目の数字, 現在の状態, 次の状態], List) infers ac
という呼ばれ方です。Listの中身はオートマトンの状態遷移表です。
この操作で、[マス目の数字, 現在の状態, 次の状態]の3つの組が、オートマトンの状態遷移表の要素のいずれかの組み合わせに一致する（それ以外の組はありえない）という制約を設定しています。

member(A,L)はご存知の通り「AはL内の要素の一つ」を表すprologの組み込み述語で、ECLiPSeの制約ではありません。
ここで使用されている「infers」というのがこのブログでも何度か触れたpropiaという仕組みで、任意のprologの述語（組み込み述語でも自作述語でも良い）をECLiPSeの制約に変換してしまうというすごい強力な仕組みです。memberは本来バックトラックを発生させてしまうため制約としては使用できないのですが、propiaを使用することにより「AはL内の要素」という意味の制約として機能するようになります。
infers ac の acの部分は制約伝搬の際にどの程度絞り込むか（候補の枝狩り）の動作に関連します。
acはarc consistency の略でアーク整合のことで、これは制約プログラミングの用語です。自分はぼんやりとしか把握してないのですがそのうちちゃんと理解したら記事書こうと思います。
infersのマニュアルページ

ちなみにECLiPSeは主にアーク整合アルゴリズムAC-3とAC-5を使用しているらしいです。

制約を作るときにオートマトンを使用するというのは面白いアイデアで今後何らかの参考になるかもしれません。

Nonogram Solverは今回解説したオートマトン使用したものの他にECLiPSeメイン開発者のJoachim Schimpfさんが作成したgecodeバージョンがあり、こちらのほうが記述が簡潔なのでそのうち解析してみたいです。

Prologの差分リスト(difference list)に関して

Leave a reply

差分リスト(difference list)の解説をします。

まず初めにPrologの通常のリストの構造の解説から。

Prologでは例えば[a,b,c,d]で表されるリストは、内部的には以下の形の木構造で表されています。

左の要素に値が入っていて、右の要素には続く要素が入るリストが入っています。黄色のところ見るとわかるように、最後の要素が[]の空リストになっています。

ここで、このリストそのものの後ろに何か新しい要素やリストを追加する方法を考えてみます。
結論から言うと、Prologでは自由変数に値を設定すると固定化されバックトラック以外の方法では変更できないため、図の黄色の空リストが入っている変数の値を変更することが出来ず、「できない」 のです。

appendという術語を用いて、append([a,b],[c,d],NewList).　のように記述するとNewListには[a,b,c,d]というリストが入りますが、前の方のリスト[a,b]はそのまま使用できず全要素コピーされています。

述語appendの定義：
append([], L, L).
append([H|T], L, [H|R]) :-
append(T, L, R).

長いリストの後ろにリストを追加するときなどは、元のリストは全要素コピーされ、結構な無駄（リスト終わりまでたどり着く時間とコピーで使用されるメモリ資源）となります。

ここで登場するのが差分リストです。
差分リストは、上記で述べた通常のリストの黄色い部分を「空リストではなく、値を決定しない自由変数のままにした」リストのことを言います。

当たり前ですが、黄色の変数に空リストを設定すると、通常のPrologのリストと全く同じになります（→差分リストを通常のリストに変換するのは簡単）
青い部分を差分リストの頭部(Head)、黄色の部分を差分リストの尾部(Tail)と言います。

差分リストの表現方法はいくつかあるようですが、自分は[Head,Tail]という表記を使用しています。
最終要素の自由変数をTailとして表に引っ張り出してきます。

無理やり図で表すとこんな感じです（便宜的に矢印つけました）

ちょっとわかりずらいので、ドット演算子をはしょって以下のように図示してみます。

この表現にすると、リストの後ろに新たなリストを追加するという操作が、「尾部の自由変数に追加したいリストを代入してやる」操作で行えることがわかります。これはappendによる1つ目のリストの全要素コピーが行われないため、高速です。

注意点としては、「新しく追加するリストの最終要素も自由変数である必要がある」「その自由変数が結合後のリストの新たな尾部となる」ということです。以下で説明します。

差分リストの結合は以下のような述語を用いて行います。
append_difference_list([List1Head, List1Tail], [List2Head, List2Tail], [List1Head, List2Tail]):-
List1Tail=List2Head.

仮に
List1:[a,b,c,d,自由変数1]
List2:[e,f,g,h,自由変数2]
とします（ちょっと表現変ですがニュアンスで）

①一番目と二番目の引数として以下のようにマッチングされます。

②List1Tail=List2Head.　の記述により List1の尾部(自由変数1)にList2が設定され、List1が以下のようなリストになります。

③3番目の引数として結合した差分リストを返します。

実際は
List1Tail=List2Head.の記述は述語を以下のような記述にすることにより省略できます。説明のためわざとこのような記述にしました。
append_difference_list([List1Head, List2Head], [List2Head, List2Tail], [List1Head, List2Tail]).

差分リストの具体的な使われ方なのですが、例えばSWI-Prologのfindall/4があります。
これは通常のfindall/3で返ってくるリストを差分リストとして返すもので、リストの尾部が4番目の引数として返ってきます。

私は以前スライドパズルのラッシュアワー(RUSH HOUR)のソルバーを作成したときにこのfindall/4を使用しました。
ソースコード
 ドキュメントおよび実行結果

詳細の解説は行いませんが、このソースコードでは幅優先探索というアルゴリズムを用いていて、ある局面から発生しうるすべての局面を生成するのにfindall/4を使用しています。結果を差分リストで取得することにより、幅優先探索キューの尾部にfindall/4で返された差分リストをそのまま追加することにより処理を効率化しています。

差分リストが使用されている他の例は構文解析などで使用される DCG(Definite clause grammar)などがあります。SWI-PrologでDCGで何らかの述語（トークン？）を記述したのちlistingなどで定義を見ると、すべて差分リストの引数が追加された同名のprolog述語に変換されているのがわかります。

Project Euler 46

Leave a reply

久しぶりに解きました。
あんまり良いプログラムではないけど…

Problem 46(日本語)
Problem 46(本家サイト)

%problem 46
:-lib(ic).
solve:-
	PrimeMax is 100000,
	assert(max(PrimeMax)),
	make_list(PrimeMax,Lst),
	eratosthenes_sieve(Lst,PrimeLst), % エラトステネスのふるいによる素数列挙

	Prime1#::PrimeLst,
	Prime2#::PrimeLst,
	A#=Prime1*Prime2,
	A#=_*2+1, % Aは奇数
	indomain(A,min),
	(
		Prime#::PrimeLst,
		B#>0,
		(A-Prime)/2 #= B*B,
		
		labeling([B])->
		(
%			printf(output,"%d = %d + 2*%d^2\n",[A,Prime,B]),
%			flush(output)
			true
		);
		(
			labeling([Prime1,Prime2]),
			printf(output,"answer %d = %d * %d\n",[A,Prime1,Prime2]),
			flush(output),
			abort
		)
	),
	fail.

mk_lst([],_,[]):-!.
mk_lst([First|Rest],Th,[Rest]):-
	First>Th,
	mk_lst(Rest,Th,Rest).
mk_lst([First|Rest],Th,[First|Rest]):-
	mk_lst(Rest,Th,Rest).

% 2 ～ Idx までのリストを作成
make_list(Idx,List):-
make_list_sub(Idx,List,[]).

make_list_sub(1,Ret,Ret):-!.
make_list_sub(Idx,Ret,List):-
Idx1 is Idx - 1,
make_list_sub(Idx1,Ret,[Idx | List]).

% 素数列挙 エラトステネスのふるい
eratosthenes_sieve([],[]):-!.
eratosthenes_sieve([First | Rest],[First | Rest]):-
max(Max),
First * First > Max ,
!.
eratosthenes_sieve([First | Rest], [First | Ret]):-
erase_baisu(First,Rest,Rest1),
eratosthenes_sieve(Rest1,Ret).

erase_baisu(_,[],[]):-!.
erase_baisu(Base,[First | Rest],[First | Ret]):-
First mod Base =\= 0,
!,
erase_baisu(Base,Rest,Ret).
erase_baisu(Base,[_ | Rest],Ret):-
erase_baisu(Base,Rest,Ret).

%problem 46

:-lib(ic).

solve:-

PrimeMax is 100000,

assert(max(PrimeMax)),

make_list(PrimeMax,Lst),

eratosthenes_sieve(Lst,PrimeLst), % エラトステネスのふるいによる素数列挙

Prime1#::PrimeLst,

Prime2#::PrimeLst,

A#=Prime1*Prime2,

A#=_*2+1, % Aは奇数

indomain(A,min),

(

Prime#::PrimeLst,

B#>0,

(A-Prime)/2 #= B*B,

labeling([B])->

(

% printf(output,"%d = %d + 2*%d^2\n",[A,Prime,B]),

% flush(output)

true

);

(

labeling([Prime1,Prime2]),

printf(output,"answer %d = %d * %d\n",[A,Prime1,Prime2]),

flush(output),

abort

)

fail.

mk_lst([],_,[]):-!.

mk_lst([First|Rest],Th,[Rest]):-

First>Th,

mk_lst(Rest,Th,Rest).

mk_lst([First|Rest],Th,[First|Rest]):-

mk_lst(Rest,Th,Rest).

% 2 ～ Idx までのリストを作成

make_list(Idx,List):-

make_list_sub(Idx,List,[]).

make_list_sub(1,Ret,Ret):-!.

make_list_sub(Idx,Ret,List):-

Idx1 is Idx - 1,

make_list_sub(Idx1,Ret,[Idx | List]).

% 素数列挙エラトステネスのふるい

eratosthenes_sieve([],[]):-!.

eratosthenes_sieve([First | Rest],[First | Rest]):-

max(Max),

First * First > Max ,

eratosthenes_sieve([First | Rest], [First | Ret]):-

erase_baisu(First,Rest,Rest1),

eratosthenes_sieve(Rest1,Ret).

erase_baisu(_,[],[]):-!.

erase_baisu(Base,[First | Rest],[First | Ret]):-

First mod Base =\= 0,

erase_baisu(Base,Rest,Ret).

erase_baisu(Base,[_ | Rest],Ret):-

erase_baisu(Base,Rest,Ret).

実行結果(回答伏せます) solve. answer XXXX = XXXX * XXXX Aborting execution ...

CHRをGPUで実行させる論文を読みました。

Leave a reply

Parallel Execution of Constraint Handling Rules on a Graphical Processing Unit
という論文を読みました。
リンク
リンク切れている場合は論文名で検索してください。

Constraint Handling Rulesの開発者のThom Fr¨uhwirth さん達が書いた論文で、CHRをGPU上で実行させる方法がCUDAのコード込みで書いてあります。

Constraint Handling Rulesに関して自分がわかっているレベル(≒あまりわかっていない)で簡単に説明すると、CHRは基本的には記述された一連の制約を論理的に同等かつよりシンプルなものにしたり、何かに変換（自作の制約で書いた記述 → 組み込み述語のみ使用した記述に変換など）したりします。

例えばECLiPSeではPropiaとは別にCHRを使用しても自作の制約が定義出来ます。

まず以下の3種類のいずれかの構文でルールを記述しておきます。(これが自作制約となります)
CHRには以下の3つしかルールがありません。
・simplification
　　Head1,Head2 <=> Guard | Body
・propagation
　　Head1,Head2 => Guard | Body
・simpagation
　　Head1¥Head2 <=> Guard | Body
（HeadもGuardもBodyも普通のPrologのCallable Termで書きます。
GuardとBodyの部分は複数の述語を書いて良い。Headの部分は最大2つの述語のみ（ECLiPSeの場合。3つ以上が不可なのは以下に述べる述語のピックアップの際の効率の問題らしいです）→すみません訂正します。CHRの昔のライブラリでは2つのみでしたが、新しいECHライブラリでは3つ以上可能でした）

動作の仕組みなのですが、上記で定義した制約を含む述語群を連言（=AND。カンマ区切りの普通のPrologの表現）で記述すると、CHRの機構はそれらの述語群の中から2つピックアップし、
・上記のHead1,Head2にパターンマッチ
・GuardがTrueとなる
を満たすものを見つけると、以下のルールに従ってピックアップした2つの述語を「書き替えて」しまいます（これをfire[発火]と呼ぶ）そしてその際にBodyの実行可能な述語は実行してしまいます。
また、Guardの部分は常時チェックされる番犬のような動作をしていて、例えばguardにnonvar(A)みたいな記述をしていた際、別の処理でAに何か値を設定した場合、その瞬間にGuardのチェックが通り対応するBodyが発火されます（ECLiPSeのsuspend機構を使って実装されている）
simplificationの場合はBodyに書き換え
propagationの場合はHead1,Head2そのままでBodyの述語を追加
simpagationはHead2のみBodyに書き換え(Head1は残す)

上記の変換を適用できるルールがなくなるまで繰り返す（2つ述語ピックアップ→Head1,Head2にマッチングするかチェック→GuardがTrueかチェック→ルールに従いHead1,Head2を書き換え）
どうも書き換え中のルール群をconstraint storeと呼んでいるようです。

ちなみに上記一連の処理中にはバックトラックは発生しません。
CHRの動作を「コミッテドチョイス」と言うらしいのですが、CHRの機構がどの述語をピックアップするか勝手に決めるのでプログラマはコントロールできない（選択を委託する）という意味かもしれません。
また、Headの部分は２つじゃなくて1つでも良いです。

CHRは基本的には上記の書き換えを行うのみなので、用途は特に制約の表現のみにとどまらず、サンプルを見ると
　最大公約数の計算
　ガウスの消去法
　高速フーリエ変換
　マージソート
など、色々な応用があります。

めちゃめちゃ端折ってますが上記がCHRの基本動作です。

記述した制約群をどのような組み合わせでピックアップ・変換したとしても必ず最終的に生成される述語群が同じになるようなとき、Confluence（合流）性を持つと言うそうです。

Confluence性はどのようにすれば担保されるかなのですが、以下の論文に書いてありますが自分はまだ理解できていない（論理学の用語がたくさん使用されてて難しいため）どうも冗長なルールを追加することにより合流性が担保されるようです。

Theory and practice of constraint handling rules
リンク切れしている場合は論文名で検索してください。

Confluence性を満たす場合CHRが並列処理に非常に向いているとのことで、理屈では確かにそうだなと自分も納得しました。

前置きが長くなりましたが、上記を踏まえたうえでGPUでCHRを使った上記の論文を読んだわけです（GPUは数千コア積んでいるものもあり単純な計算を同時に行うのに非常に有力）
論文の内容はCUDAコードが実際に記載されていて実装イメージがしやすいものでした。
しかし、ルールの述語自体をCUDAコンパイル用のコードで書いているため、あまり汎用性がないのではないという気がしました。
使う側は当然任意の述語を使いたいのですが、論文のやり方ではそのたびに新たなプログラムをCUDA用に書いてコンパイルしなくてはならないのでは？と感じました。
あまりGPUのことわかってないですが、if文を多用するプログラムは遅くなるなど、性能を100%出すためにいろいろ条件があるようです。
現状ではCHRをGPUの速度を100%出し切って実行するのは難しいのかな、と感じました。
ただ理論的にCHRのいろいろな性質が証明されているので、ハードウェア側でCHRに向いた実装が実現されたら、かなり望みがあるような気がします。

余談ですが「CHRには3つしかルールがない」と書きましたが、
・simpagation
　　Head1¥Head2 <=> Guard | Body
の、
・simplification はこれの Head1 がないバージョン（Head2がBodyに書き換えられる)
・propagation はこれの Head2 がないバージョン(Head1そのままでBodyが追加される)
となるので実質はsimpagationだけで良いみたいな文章をどこかで読みました。