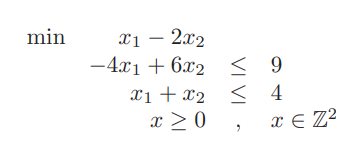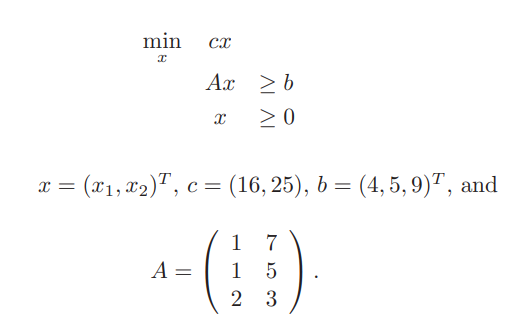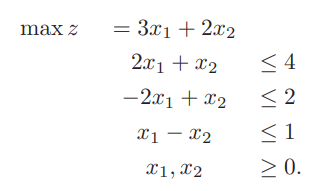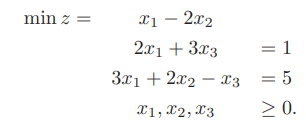以下のGitHubページにソースコードを掲載しましたがこちらにも書きます。
GitHubリンク
2次元板取り問題というのは、例えば10×10のサイズの紙があったとして、幅と高さが以下のサイズの紙片を切り抜きたいときどのように切り抜くことが可能かを解く問題です。
3×3
2×1
6×7
5×2
使い方
|
1 |
eclipse -f cuttingstock2d.ecl -e "solve_cutting_stock_2d(入力CSVファイルパス,出力CSVファイルパス)" |
(ECLiPSeの実行ファイルのパスを前もって環境変数PATHに設定しておく必要あり)
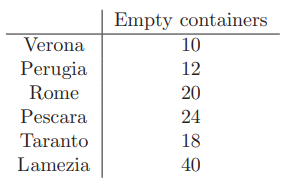
入力CSVファイルフォーマット(すべての数字は整数の必要あり):
1行目: 紙の幅, 紙の高さ
2行目: 紙片1の幅, 紙片1の高さ
3行目: 紙片2の幅, 紙片2の高さ
…
出力CSVファイルフォーマット:(紙片が90度回転している可能性あり、y座標は下方向に増加)
1行目: 紙片1の左のx座標,紙片1の上のy座標,紙片1の幅, 紙片1の高さ
2行目: 紙片2の左のx座標,紙片2の上のy座標,紙片2の幅, 紙片2の高さ
…
例
in.csvの中身:
|
1 2 3 4 5 |
10,10 3,3 2,1 6,7 5,2 |
実行コマンド:
|
1 |
eclipse -f cuttingstock2d.ecl -e "solve_cutting_stock_2d('in.csv','out.csv')" |
標準出力:
|
1 2 3 4 5 6 7 8 9 10 |
1 1 1 4 4 4 4 4------ 1 1 1 4 4 4 4 4------ 1 1 1--------------------- 2 3 3 3 3 3 3--------- 2 3 3 3 3 3 3--------- --- 3 3 3 3 3 3--------- --- 3 3 3 3 3 3--------- --- 3 3 3 3 3 3--------- --- 3 3 3 3 3 3--------- --- 3 3 3 3 3 3--------- |
out.csv の出力:
|
1 2 3 4 |
0,0,3,3 0,3,1,2 1,3,6,7 3,0,5,2 |
注意:このプログラムは内部的にバックトラックにより別解を求めることが可能ですが、上記の使用方法では最初の解しか得られません。ECLiPSe外部からの使用で別解が欲しい場合はPHPやPythonから呼ぶライブラリの使用を検討してください
ソースコード(cuttingstock2d.ecl)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
:- lib(ic). :- lib(csv). solve_cutting_stock_2d(InCSV,OutCSV):- csv_read(InCSV, CsvRows, []), CsvRows = [[CWidth,CHeight]|Panels], (foreach(CsvPanel,Panels),fromto(PanelVars,[Panel|RestPanels],RestPanels,[]),param(CWidth,CHeight) do ( [CsvWidth,CsvHeight] = CsvPanel, Width#>=0, Height#>=0, (Width #= CsvWidth and Height #= CsvHeight) or (Width #= CsvHeight and Height #= CsvWidth), LeftX #:: 0..CWidth, TopY #:: 0..CHeight, 0 #=<LeftX, LeftX #=< CWidth-Width, 0 #=<TopY, TopY #=< CHeight-Height, Panel = [](LeftX,TopY,Width,Height) ) ), (fromto(PanelVars,[PickedupPanel|RestPanelVars],RestPanelVars,[]) do (foreach(CheckPanel,RestPanelVars),param(PickedupPanel) do PickedupPanel = [](LeftX1,TopY1,Width1,Height1), CheckPanel = [](LeftX2,TopY2,Width2,Height2), ( LeftX2+Width2 #=< LeftX1 or LeftX1 + Width1 #=< LeftX2) or ( TopY2+Height2 #=< TopY1 or TopY1 + Height1 #=< TopY2) ) ), term_variables(PanelVars,Flatten), labeling(Flatten), %visualization, csv out open(OutCSV, write, OutStrm), dim(VisDim,[CWidth,CHeight]), ( foreach([](Left,Top,Width,Height),PanelVars),count(Idx,1,_),param(VisDim,OutStrm) do write(OutStrm,Left),write(OutStrm,","), write(OutStrm,Top),write(OutStrm,","), write(OutStrm,Width),write(OutStrm,","), writeln(OutStrm,Height), ( for(Y,Top+1,Top+Height),param(VisDim,Idx,Width,Left) do ( for(X, Left+1, Left+Width),param(VisDim,Y,Idx) do %VisDim[X,Y] = Idx arg([X,Y], VisDim, Idx) ) ) ), ( for(Y,1,CHeight),param(VisDim,CWidth) do (for(X, 1, CWidth),param(VisDim,Y) do arg([X,Y], VisDim, Elem), nonvar(Elem)->printf("%3d",[Elem]);printf("---",[]) ), nl ), close(OutStrm). |
このプログラムではラベリング(制約変数への値の割り当て)をlabeling/1の使用のみとしてサボっています(値を割り当てる変数の選択はリストの先頭から順に、割り当てる値はドメインの最小値から1つづつ増やしていく)。
・ラベリングする変数の選択
・変数への値の割り当て方
を細やかに制御することにより探索速度アップの余地があります。
例えば「よりサイズの大きい紙片の位置から先に決定」のようなラベリング方法にすると速度の改善がみられるかもしれません。
制約論理プログラミングでは「制約の記述」と「ラベリング順の記述」が完全に分離しているため、思いついたラベリング順のアイデアを簡単に試すことができます。labeling/1をコールするのが一番手を抜いた方法となります。
ラベリング順の制御に関しては以下を参考にしてみてください。
labelingに関して
ECLiPSe CLPのsearch/6のChoiceの実験
ECLiPSe tutorial.pdfのTree Search MethodsのChapter
ECLiPSe e-learning course の Chapter 6 Search Strategies N-Queen Puzzle