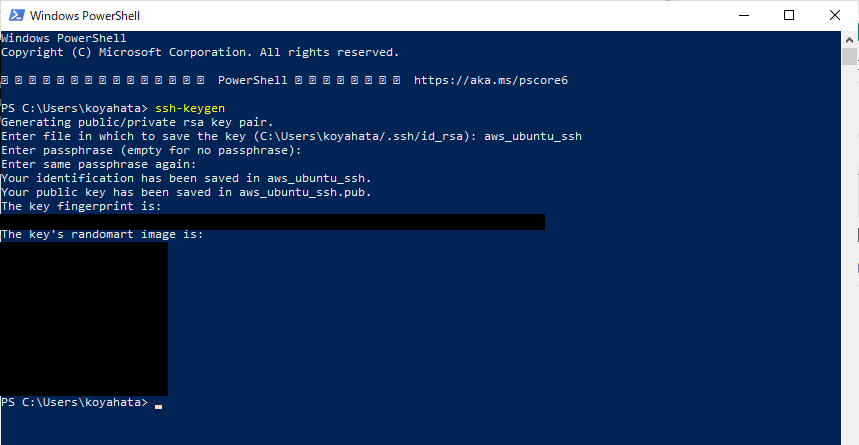
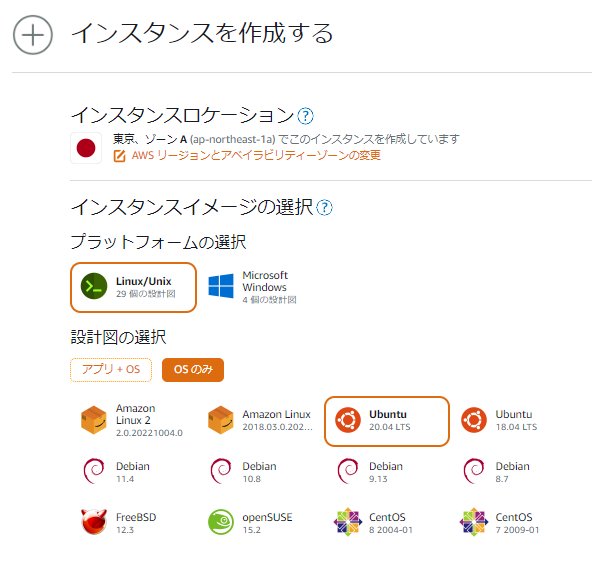
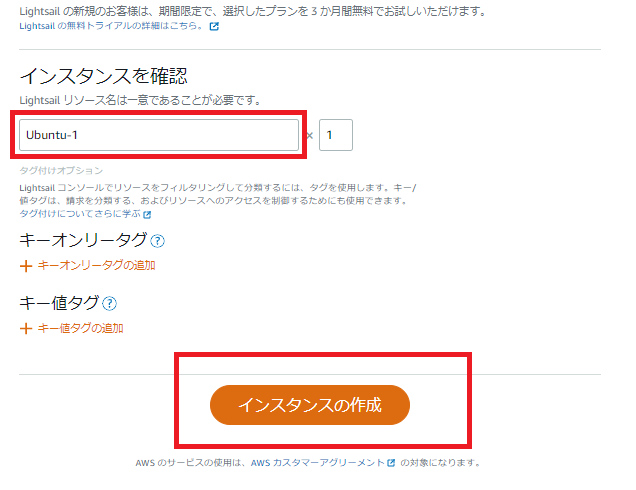
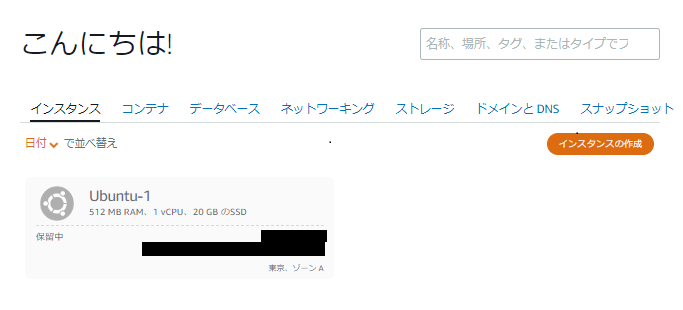
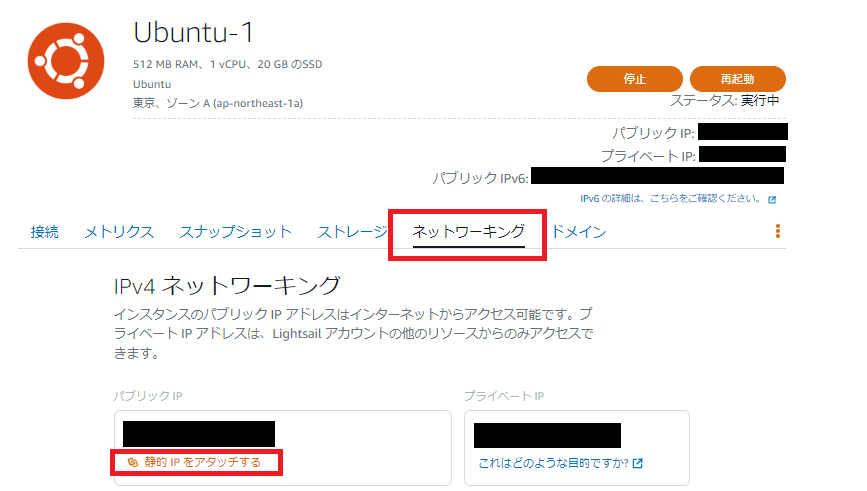
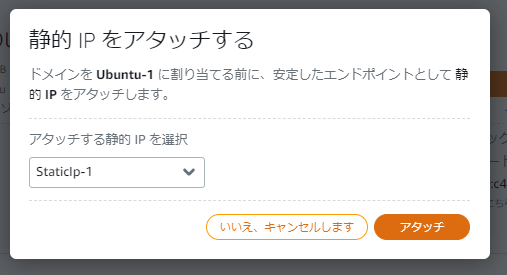
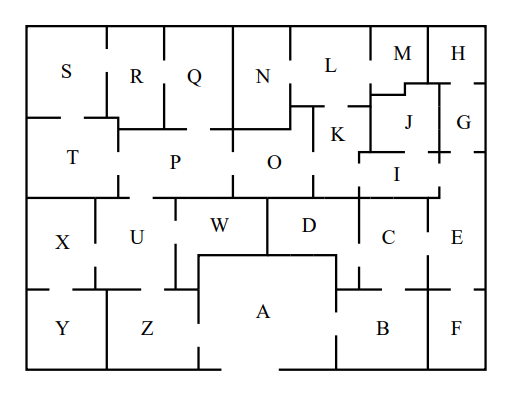
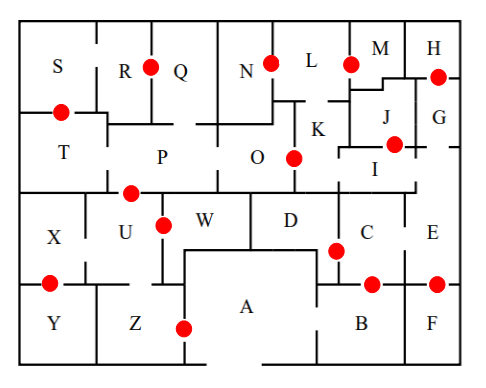
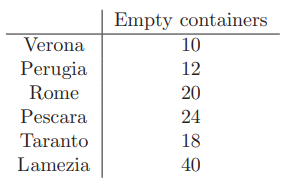
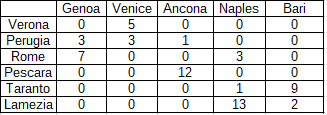
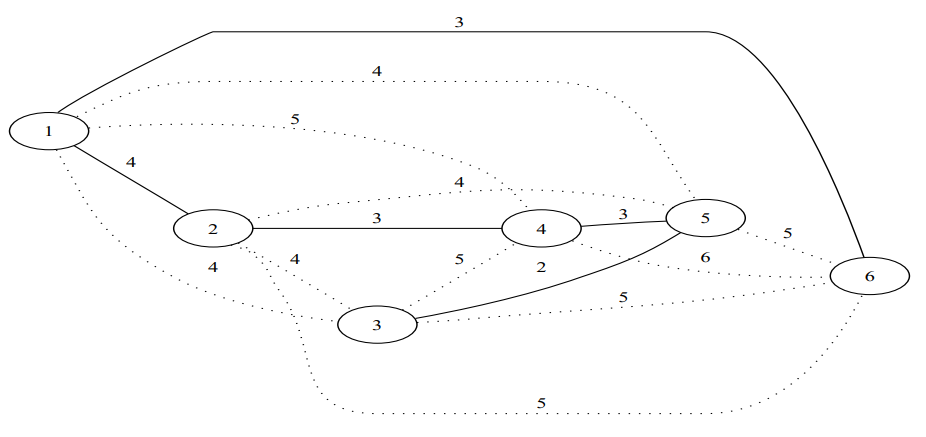
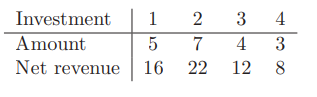小屋畑ソフトウェアサービスブログページ

Project Euler 117

https://odz.sakura.ne.jp/projecteuler/index.php?Problem+117

考え方は116と大体同じ。

多分動的計画法だかメモ化？だかを実装しているような気がする…（使用しているアルゴリズムの名前をわかってない）

116、117あたりはChatGPTでもするっと解けそう

回答は省略

%problem117
:- dynamic combination_count_assert/3.

%combination_count_assert(tile_rest, most_left_block_size, combination_count).

solve:-
	retractall(combination_count_assert(_,_,_)),
	combination_count(50, 1, CombinationCount1),
	combination_count(50, 2, CombinationCount2),
	combination_count(50, 3, CombinationCount3),
	combination_count(50, 4, CombinationCount4),
	Answer is CombinationCount1 + CombinationCount2 + CombinationCount3 + CombinationCount4, 
	printf(output,"answer = %d = %d + %d + %d + %d\n",[Answer,CombinationCount1,CombinationCount2,CombinationCount3,CombinationCount4]).

combination_count(RestTiles, BlockSize, CombinationCount):-
	combination_count_assert(RestTiles,BlockSize,CombinationCount),!.	% メモしたケースにヒット
combination_count(RestTiles, BlockSize, CombinationCount):-
	RestTiles - BlockSize =:= 0,
	CombinationCount = 1,
	!.
combination_count(RestTiles, BlockSize, CombinationCount):-
	RestTiles - BlockSize < 0,
	CombinationCount = 0,
	!.
combination_count(RestTiles, BlockSize, CombinationCount):-
	RestTiles1 is RestTiles - BlockSize,
	combination_count(RestTiles1, 1, CombinationCount1),	% 一番左が空のケース
	combination_count(RestTiles1, 2, CombinationCount2),	% 一番左がBlock(size:2)を配置したケース
	combination_count(RestTiles1, 3, CombinationCount3),	% 一番左がBlock(size:3)を配置したケース
	combination_count(RestTiles1, 4, CombinationCount4),	% 一番左がBlock(size:4)を配置したケース
	
	CombinationCount is CombinationCount1 + CombinationCount2 + CombinationCount3 + CombinationCount4,
	assert(combination_count_assert(RestTiles, BlockSize, CombinationCount)).

2026年2月22日

Project Euler 116

https://odz.sakura.ne.jp/projecteuler/index.php?Problem+116

久しぶりにProject Euler解きました。競技プログラミングはChatGPTなどの登場でかなり下火になってるらしいですが。ただ自分が解き済みの問題やらせてみたら全然正答できないのもありますね。

答えなどは省略

%problem116
:- dynamic combination_count_assert/3.

%combination_count_assert(tile_rest,block_size,combinatin_count).

solve:-
retractall(combination_count_assert(,,_)),
combination_count(50, 2, CombinationCount2),
combination_count(50, 3, CombinationCount3),
combination_count(50, 4, CombinationCount4),
Answer is CombinationCount2 + CombinationCount3 + CombinationCount4 – 3,
printf(output,”answer = %d = %d + %d + %d – 3\n”,[Answer,CombinationCount2,CombinationCount3,CombinationCount4]).

combination_count(RestTiles, BlockSize, CombinationCount):-
combination_count_assert(RestTiles,BlockSize,CombinationCount),!. % メモしたケースにヒット
combination_count(0, , 1):-!. combination_count(RestTiles, , 0):-
RestTiles<0,
!.
combination_count(RestTiles, BlockSize, CombinationCount):-
RestTiles1 is RestTiles – BlockSize,
combination_count(RestTiles1, BlockSize, CombinationCount1), % 一番左にBlockを配置したケース
RestTiles2 is RestTiles – 1,
combination_count(RestTiles2, BlockSize, CombinationCount2), % 一番左が空のケース
CombinationCount is CombinationCount1 + CombinationCount2,
assert(combination_count_assert(RestTiles, BlockSize, CombinationCount)).

2026年2月21日
AWS Lightsail で tftp接続を行う

AWS Lightsailのインスタンス生成からTftpで接続しファイル転送が行える状態までもっていく手順

サーバー:Ubuntu 20.04 LTS
クライアント：Windows 10
TFTPクライアント：FileZilla

大まかな流れ
①AWS LightsailのUbuntu20.04 LTSのインスタンス作成
②WindowsのPowerShellにて鍵ペア作成
③UbuntuにSSH接続して公開鍵を貼り付け
④FileZillaで接続

まずインスタンスを作ります。

出来上がったインスタンスをクリック

静的IPアドレスが再起動などで変更されないようアタッチする

とりあえずサーバの方はこのまま置いておいて、Windowsでの鍵ペア生成の作業に移ります。

Powershellを起動し以下を行います。
1.ssh-keygen
2.キー名称を設定
3.パスフレーズの設定（覚えておく）

鍵ペアができました。「～.pub」のほうが公開鍵、そうでない方が秘密鍵となります。
「～.pub」のほうをテキストエディタで開いてコピーします。

Ubuntu作業に戻ります。以下の操作でSSHコンソールを開きます。

/home/ubuntu/.ssh　に移動し、　authorized_keyを開き、先ほどエディタでコピーした公開鍵の情報を貼り付けます。

Windows作業に戻ります。FileZillaをインストールして開きます。
AWSサーバーの情報を設定しキーは先ほど作成した秘密鍵を参照します。

秘密鍵の形式がFileZillaで対応してないとのことで、言われるがまま変換。

接続します。

接続できました。

2022年11月14日
Now I’m searching for remote jobs of overseas which can be done while living in Japan

To engineer readers working in foreign company (not Japan)

I live in Hokkaido, Japan(GMT+9) and am looking for a full remote software development job of overseas which can be done while living in Japan (I’m not searching for Japanese domestic jobs).
I have worked over 20 years as a software engineer.
have bachelor degree of computer science.
can work from December 1st, 2022.

I appreciate you letting me know if you have any opportunities for me.
Please share this post and comment for better reach.

Though currently I’m interested in Prolog and Constraint Logic Programming,
I have many experiences of other technologies and will be glad to take charge in those:
-Mobile apps(Android/iPhone), Google Map API, WebView
-Web App(PHP, JavaScript[Angular.js, Fabric.js, Leaflet.js, jQuery, and more])
-Image Processing(OpenCV)
-databases(MySQL, PostgreSQL, Oracle, Microsoft ACCESS)
-Embedded Software, Firmware (development of sensor drivers, RTOS)
-Linear Algebra

my resume:
Link

Stack overflow:
Link

Github page(now I’m migrating my blog post’s programs into here):
Link

Project Euler

My skills
Language: C, C++, C#, VB.net, PHP, JavaScript(fabric.js, leaflet.js, Angular.js, jQuery, Ajax), Java, Swift, Prolog, HTML, CSS, VB6, VBA, and VB.net
Database: SQL Server, MS-ACCESS, Oracle, MySQL, PostgreSQL
Technology and other: web programming, database software, embedded software, RTOS, image processing, OpenCV, linear algebra, android/iPhone application, Linux(Ubuntu, CentOS, Raspberry Pi), Google Map API, MFC

Please send me email(koyahata@koyahatataku.com) if you have any opportunities.
Any help will be appreciated.

2022年10月31日
ECLiPSe CLPで2次元の板取り問題(2d cutting stock problem)を解く
以下のGitHubページにソースコードを掲載しましたがこちらにも書きます。
GitHubリンク

2次元板取り問題というのは、例えば10×10のサイズの紙があったとして、幅と高さが以下のサイズの紙片を切り抜きたいときどのように切り抜くことが可能かを解く問題です。
3×3
2×1
6×7
5×2

使い方
```
eclipse -f cuttingstock2d.ecl -e "solve_cutting_stock_2d(入力CSVファイルパス,出力CSVファイルパス)"
```
（ECLiPSeの実行ファイルのパスを前もって環境変数PATHに設定しておく必要あり)

入力CSVファイルフォーマット(すべての数字は整数の必要あり):
1行目: 紙の幅, 紙の高さ
2行目: 紙片1の幅, 紙片1の高さ
3行目: 紙片2の幅, 紙片2の高さ
…

出力CSVファイルフォーマット:(紙片が90度回転している可能性あり、y座標は下方向に増加)
1行目: 紙片1の左のx座標,紙片1の上のy座標,紙片1の幅, 紙片1の高さ
2行目: 紙片2の左のx座標,紙片2の上のy座標,紙片2の幅, 紙片2の高さ
…

例
in.csvの中身:
```
10,10
3,3
2,1
6,7
5,2
```
実行コマンド:
```
eclipse -f cuttingstock2d.ecl -e "solve_cutting_stock_2d('in.csv','out.csv')"
```
標準出力:
```
  1  1  1  4  4  4  4  4------
  1  1  1  4  4  4  4  4------
  1  1  1---------------------
  2  3  3  3  3  3  3---------
  2  3  3  3  3  3  3---------
---  3  3  3  3  3  3---------
---  3  3  3  3  3  3---------
---  3  3  3  3  3  3---------
---  3  3  3  3  3  3---------
---  3  3  3  3  3  3---------
```
out.csv の出力:
```
0,0,3,3
0,3,1,2
1,3,6,7
3,0,5,2
```
注意：このプログラムは内部的にバックトラックにより別解を求めることが可能ですが、上記の使用方法では最初の解しか得られません。ECLiPSe外部からの使用で別解が欲しい場合はPHPやPythonから呼ぶライブラリの使用を検討してください

ソースコード（cuttingstock2d.ecl）
```
:- lib(ic).
:- lib(csv).

solve_cutting_stock_2d(InCSV,OutCSV):-

	csv_read(InCSV, CsvRows, []),
	CsvRows = [[CWidth,CHeight]|Panels],

	(foreach(CsvPanel,Panels),fromto(PanelVars,[Panel|RestPanels],RestPanels,[]),param(CWidth,CHeight) do
		(
			[CsvWidth,CsvHeight] = CsvPanel,
			Width#>=0,
			Height#>=0,
			(Width #= CsvWidth and Height #= CsvHeight) or 
			(Width #= CsvHeight and Height #= CsvWidth),
			LeftX #:: 0..CWidth,
			TopY #:: 0..CHeight,
			0 #=<LeftX, LeftX #=< CWidth-Width,
			0 #=<TopY, TopY #=< CHeight-Height,
			Panel = [](LeftX,TopY,Width,Height)
		)
	),
	(fromto(PanelVars,[PickedupPanel|RestPanelVars],RestPanelVars,[]) do 
		(foreach(CheckPanel,RestPanelVars),param(PickedupPanel) do
			PickedupPanel = [](LeftX1,TopY1,Width1,Height1),
			CheckPanel    = [](LeftX2,TopY2,Width2,Height2),
			( LeftX2+Width2 #=< LeftX1 or LeftX1 + Width1 #=< LeftX2) or
			( TopY2+Height2 #=< TopY1 or TopY1 + Height1 #=< TopY2)

		)
	),
	term_variables(PanelVars,Flatten),
	labeling(Flatten),

	%visualization, csv out
	open(OutCSV, write, OutStrm),
	dim(VisDim,[CWidth,CHeight]),
	( foreach([](Left,Top,Width,Height),PanelVars),count(Idx,1,_),param(VisDim,OutStrm) do

	
		write(OutStrm,Left),write(OutStrm,","),
		write(OutStrm,Top),write(OutStrm,","),
		write(OutStrm,Width),write(OutStrm,","),
		writeln(OutStrm,Height),
		( for(Y,Top+1,Top+Height),param(VisDim,Idx,Width,Left)  do
			( for(X, Left+1, Left+Width),param(VisDim,Y,Idx) do
				%VisDim[X,Y] = Idx
				arg([X,Y], VisDim, Idx)
			)
		)
	),
	( for(Y,1,CHeight),param(VisDim,CWidth)  do
		(for(X, 1, CWidth),param(VisDim,Y) do
			arg([X,Y], VisDim, Elem),
			nonvar(Elem)->printf("%3d",[Elem]);printf("---",[])
		),
		nl
	),
	close(OutStrm).
```
このプログラムではラベリング（制約変数への値の割り当て）をlabeling/1の使用のみとしてサボっています（値を割り当てる変数の選択はリストの先頭から順に、割り当てる値はドメインの最小値から１つづつ増やしていく）。
・ラベリングする変数の選択
・変数への値の割り当て方
を細やかに制御することにより探索速度アップの余地があります。
例えば「よりサイズの大きい紙片の位置から先に決定」のようなラベリング方法にすると速度の改善がみられるかもしれません。

制約論理プログラミングでは「制約の記述」と「ラベリング順の記述」が完全に分離しているため、思いついたラベリング順のアイデアを簡単に試すことができます。labeling/1をコールするのが一番手を抜いた方法となります。

ラベリング順の制御に関しては以下を参考にしてみてください。
labelingに関して
 ECLiPSe CLPのsearch/6のChoiceの実験
 ECLiPSe tutorial.pdfのTree Search MethodsのChapter
ECLiPSe e-learning course の Chapter 6 Search Strategies N-Queen Puzzle
2022年10月28日

ECLiPSe CLPで美術館の警備員配置問題を解く

ECLiPSe CLPで以下の美術館の警備員配置問題を解きます。

問題（Problems and exercises in Operations Researchの4.7 Museum Guards）:

以下のような部屋構成の美術館に警備員を配置せよ。

条件：
・コスト削減のため警備員は各部屋をつなぐドアの位置に配置し2つの部屋を同時に警備する。
・どの部屋も少なくとも1人の警備員が見張っているようにする。
・上記条件を満たしつつ、なるべく少ない警備員で警備する。

プログラム：

:-lib(ic).
:-lib(branch_and_bound).

solve(Vars):-
	Graph = 
	[](
		[](a,b,N1),
		[](a,g,N2),
		[](a,f,N3),
		[](a,c,N4),
		[](b,h,N5),
		[](c,d,N6),
		[](d,e,N7),
		[](d,f,N8),
		[](g,i,N9),
		[](h,i,N10),
		[](i,j,N11)
	),
	
	Nodes = [a,b,c,d,e,f,g,h,i,j],
	Vars=[N1,N2,N3,N4,N5,N6,N7,N8,N9,N10,N11],
	Vars#::0..1,
		
	(
		foreach(Node,Nodes),param(Graph)
		do
		(
			(
				foreacharg([](P1,P2,P3),Graph), fromto(0,In,Out,OutFormula), param(Node)
				do
				(
					P1==Node->
						Out = In+P3;
						(
							P2==Node->
								Out=In+P3;Out=In
						)
				)
			),
			ic:(eval(OutFormula)#>=1)
		)
	),
	ic:(Sum #= sum(Vars)),
	bb_min(labeling(Vars),Sum,bb_options{timeout:60,solutions:all}).

実行結果：

?- solve(Ans).
Ans = [0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1]
Yes (0.00s cpu, solution 1, maybe more)
Ans = [0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1]
Yes (0.00s cpu, solution 2, maybe more)
Ans = [0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1]
Yes (0.00s cpu, solution 3, maybe more)
Ans = [0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1]
Yes (0.00s cpu, solution 4, maybe more)
Ans = [0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1]
Yes (0.00s cpu, solution 5, maybe more)
Ans = [0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1]
Yes (0.00s cpu, solution 6, maybe more)
Ans = [0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1]
Yes (0.00s cpu, solution 7, maybe more)
No (0.00s cpu)

Found a solution with cost 6
Found no solution with cost 2.0 .. 5.0

解答配置（の一つ）

解説：
まず部屋をノード、ドアをエッジと考えたグラフを作成し、エッジごとに警備員がいるかいないかを表す変数を宣言します。警備員がいれば１、いなければ０。

Nodesに全部屋のリストを用意しておいて(20行目）、
それをひとつづつ指定したループを処理します(25行目）
ループ中ではエッジ配列の中で指定した部屋を持つものを探し、警備員有無の変数をすべて足し合わせます(29行目からのループ）。ある部屋に注目したとき、そのすべてのドアに対応する警備員変数を足し合わせた式を作ります。少なくとも1つのドアには警備員がいるはずなのでこの式に「1以上」の制約をつけます（40行目）

警備員の数を最小にするのが目標なので警備員有無変数の配列Varsの合計が最小になるように指定し分枝限定法(branch_and_bound)を用いてVarsの値を求めます。
実行結果を見るとわかる通り、最小コストは６で、7つの解があるようです。

もう一つ、以下のもっと複雑な部屋割りの場合も解いてみます。

プログラム：

:-lib(ic).
:-lib(branch_and_bound).

solve(Vars):-
	Graph = 
	[](
		[](s,r,N1),
		[](s,t,N2),
		[](r,q,N3),
		[](q,p,N4),
		[](n,l,N5),
		[](l,m,N6),
		[](l,k,N7),
		[](t,p,N8),
		[](p,o,N9),
		[](o,k,N10),
		[](k,i,N11),
		[](j,i,N12),
		[](h,g,N13),
		[](g,e,N14),
		[](x,u,N15),
		[](u,w,N16),
		[](d,c,N17),
		[](i,e,N18),
		[](c,e,N19),
		[](x,y,N20),
		[](u,z,N21),
		[](z,a,N22),
		[](a,b,N23),
		[](b,c,N24),
		[](e,f,N25),
		[](p,u,N26)
	),
	
	Nodes = [a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,w,x,y,z],
	Vars=[N1,N2,N3,N4,N5,N6,N7,N8,N9,N10,N11,N12,N13,N14,N15,N16,N17,N18,N19,N20,N21,N22,N23,N24,N25,N26],
	Vars#::0..1,
		
	(
		foreach(Node,Nodes),param(Graph)
		do
		(
			(
				foreacharg([](P1,P2,P3),Graph), fromto(0,In,Out,OutFormula), param(Node)
				do
				(
					P1==Node->
						Out = In+P3;
						(
							P2==Node->
								Out=In+P3;Out=In
						)
				)
			),
			ic:(eval(OutFormula)#>=1)
		)
	),
	ic:(Sum #= sum(Vars)),
	bb_min(labeling(Vars),Sum,bb_options{timeout:60,solutions:all}),
	(
		fromto(Vars,[First|Rest],Rest,[])
		do
		write(First),write(",")
	),nl.

実行結果：

?- solve(Ans).
Ans = [0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.00s cpu, solution 1, maybe more)
Ans = [0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.02s cpu, solution 2, maybe more)
Ans = [0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.02s cpu, solution 3, maybe more)
Ans = [0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.02s cpu, solution 4, maybe more)
Ans = [0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.02s cpu, solution 5, maybe more)
Ans = [0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.02s cpu, solution 6, maybe more)
Ans = [0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.02s cpu, solution 7, maybe more)
Ans = [0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.02s cpu, solution 8, maybe more)
Ans = [0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.02s cpu, solution 9, maybe more)
Ans = [0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.02s cpu, solution 10, maybe more)
Ans = [0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.02s cpu, solution 11, maybe more)
Ans = [0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.02s cpu, solution 12, maybe more)
Ans = [0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.03s cpu, solution 13, maybe more)
Ans = [0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.03s cpu, solution 14, maybe more)
Ans = [0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.03s cpu, solution 15, maybe more)
Ans = [0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.03s cpu, solution 16, maybe more)
Ans = [0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.03s cpu, solution 17, maybe more)
Ans = [0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.03s cpu, solution 18, maybe more)
Ans = [1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.03s cpu, solution 19, maybe more)
Ans = [1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.03s cpu, solution 20, maybe more)
Ans = [1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.03s cpu, solution 21, maybe more)
Ans = [1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.03s cpu, solution 22, maybe more)
Ans = [1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.03s cpu, solution 23, maybe more)
Ans = [1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.03s cpu, solution 24, maybe more)
Ans = [1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.03s cpu, solution 25, maybe more)
Ans = [1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.03s cpu, solution 26, maybe more)
Ans = [1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, ...]
Yes (0.03s cpu, solution 27, maybe more)
No (0.03s cpu)

Found a solution with cost 14
Found no solution with cost 8.0 .. 13.0
0,1,1,0,1,1,0,0,0,1,0,1,1,0,0,1,1,0,0,1,0,1,0,1,1,1,
0,1,1,0,1,1,0,0,0,1,0,1,1,0,0,1,1,0,0,1,0,1,1,0,1,1,
0,1,1,0,1,1,0,0,0,1,0,1,1,0,0,1,1,0,0,1,1,0,1,0,1,1,
0,1,1,0,1,1,0,0,1,0,1,1,1,0,0,1,1,0,0,1,0,1,0,1,1,0,
0,1,1,0,1,1,0,0,1,0,1,1,1,0,0,1,1,0,0,1,0,1,1,0,1,0,
0,1,1,0,1,1,0,0,1,0,1,1,1,0,0,1,1,0,0,1,1,0,1,0,1,0,
0,1,1,0,1,1,0,0,1,1,0,1,1,0,0,1,1,0,0,1,0,1,0,1,1,0,
0,1,1,0,1,1,0,0,1,1,0,1,1,0,0,1,1,0,0,1,0,1,1,0,1,0,
0,1,1,0,1,1,0,0,1,1,0,1,1,0,0,1,1,0,0,1,1,0,1,0,1,0,
0,1,1,0,1,1,0,1,0,1,0,1,1,0,0,1,1,0,0,1,0,1,0,1,1,0,
0,1,1,0,1,1,0,1,0,1,0,1,1,0,0,1,1,0,0,1,0,1,1,0,1,0,
0,1,1,0,1,1,0,1,0,1,0,1,1,0,0,1,1,0,0,1,1,0,1,0,1,0,
0,1,1,0,1,1,1,0,1,0,0,1,1,0,0,1,1,0,0,1,0,1,0,1,1,0,
0,1,1,0,1,1,1,0,1,0,0,1,1,0,0,1,1,0,0,1,0,1,1,0,1,0,
0,1,1,0,1,1,1,0,1,0,0,1,1,0,0,1,1,0,0,1,1,0,1,0,1,0,
0,1,1,1,1,1,0,0,0,1,0,1,1,0,0,1,1,0,0,1,0,1,0,1,1,0,
0,1,1,1,1,1,0,0,0,1,0,1,1,0,0,1,1,0,0,1,0,1,1,0,1,0,
0,1,1,1,1,1,0,0,0,1,0,1,1,0,0,1,1,0,0,1,1,0,1,0,1,0,
1,0,0,1,1,1,0,1,0,1,0,1,1,0,0,1,1,0,0,1,0,1,0,1,1,0,
1,0,0,1,1,1,0,1,0,1,0,1,1,0,0,1,1,0,0,1,0,1,1,0,1,0,
1,0,0,1,1,1,0,1,0,1,0,1,1,0,0,1,1,0,0,1,1,0,1,0,1,0,
1,0,1,0,1,1,0,1,0,1,0,1,1,0,0,1,1,0,0,1,0,1,0,1,1,0,
1,0,1,0,1,1,0,1,0,1,0,1,1,0,0,1,1,0,0,1,0,1,1,0,1,0,
1,0,1,0,1,1,0,1,0,1,0,1,1,0,0,1,1,0,0,1,1,0,1,0,1,0,
1,1,0,1,1,1,0,0,0,1,0,1,1,0,0,1,1,0,0,1,0,1,0,1,1,0,
1,1,0,1,1,1,0,0,0,1,0,1,1,0,0,1,1,0,0,1,0,1,1,0,1,0,
1,1,0,1,1,1,0,0,0,1,0,1,1,0,0,1,1,0,0,1,1,0,1,0,1,0,

解答配置（の一つ）

最小コストは１４、全部で27通りの解があるようです。

2021年11月18日

PrologのLogical Loopの解説
ECLiPSe CLPでソルバーを作るときに欠かせないLogical Loopの説明をしたいと思います。

Prologでプログラムを書いたことがない人は信じられないと思いますが、なんとPure Prologには繰り返し処理を書くための構文がなくて、ループごとに再帰処理を使った述語を定義して繰り返し処理を行います。

例えばLstというリストに入っている要素をすべて表示するという処理を書きたい場合、以下のようにdsp_lst/1という術語を定義して繰り返しを書いて行います：
```
main:-
	Lst=[a,b,c,d,e,f],
	dsp_lst(Lst).

dsp_lst([]).
dsp_lst([First|Rest]):-
	write(First),nl,
	dsp_lst(Rest).
```
実行結果：
```
?- main.
Yes (0.00s cpu)
a
b
c
d
e
f
```
このように繰り返しの為だけに定義した述語をauxiliary predicate（補助述語）と呼ぶようです。よくPrologのコードで出てくるのですが、述語名のうしろにアンダーバーとかを1つつけて、ループ用の補助述語を定義したりします。

上記かなり愚かしい仕様に思えますが、恐らく以下のような理由からだと推測します。
①Prologの述語は本来「動作」「処理」ではなく、引数同士の「関係」を記述するためのもの（関数ではなく述語と呼ぶゆえん。一階述語論理の述語）
②例えば以下のような述語があった場合、
```
pred(A,B,C):-
	term1(A,B,C),
	term2(A,C),
	term3(A,B).
```
term1～term3のそれぞれの引数同士の関係が「すべて」成り立つとき、pred(A,B,C)が真となる。本来カンマは「処理の区切り」ではなく「複数の述語どうしを結ぶ条件の&」を表すという原則がある（orは;もしくは同名の別の述語定義)。極論を言えばterm1からterm3の順番をバラバラにしても成り立つはず（実際は大いに記述の順番に依存しますが…理想とする姿がそこという意味）、単純に複数の述語を&で結んだものに過ぎないので繰り返しとかいう概念がそもそもない。

（余談ですが制約論理プログラミングの制約「のみ」で書かれた述語は述語内の制約の順番をバラバラに並び替えても基本的に問題なく動作します。Prologの理想に近い）

このような仕様に一石を投じたのがECLiPSe CLPのメイン開発者のJoachim Schimpfさんの書いた以下の論文です。
Logical Loops
この論文によってPrologに自然な形でのループ処理の記述方法が提示され、ECLiPSeやSicstus Prologなどで採用されています。

Logical Loopの書き方は、上記の補助述語でループを書いていた人に自然に受け入れられるような仕様となっています。逆にPrologで補助述語を使ったループを書いたことがない人は使いこなすまで時間がかかるかもしれません。再帰を使用してループを記述することに慣れている必要があります。

例えば上記のLstというリスト内の文字をすべて表示するプログラムをLogical Loopで書くと、以下のようになります。
```
main:-
	Lst=[a,b,c,d,e,f],
	(
		fromto(Lst,[First|Rest],Rest,[]) do
		(
			write(First),nl
		)
	).
```
上記のように
1.fromtoなどの繰り返し制御用の記述
2.do
3.(繰り返す処理)

の3つの部分を書きます。
補助述語との比較で理解すると良いのですが、
「1.fromtoなどの繰り返し制御用の記述」→述語の引数の部分
「3.繰り返す処理」→述語の内部の処理
となります。
補助述語の書き方をそのまま置き換えたような扱いなので、「繰り返す処理」の部分は別述語のように独立となっていて、ループの外で使われている変数などは明示的に指定しない限り一切使用することはできません。使いたい場合はparamという構文を使用して引数として渡す（後述）必要があります。

fromtoの4つの引数の意味は(First,In,Out,Last)となっていて、やはり補助述語と関連付けて理解すると良いのですが
In→補助述語の引数
Out→補助述語内で再帰呼び出しする際に指定する引数
Last→補助述語の引数がこの値でコールされたらループ終了
という感じです。
一番初めに補助述語をコールする際に指定する引数がFirstとなります。

駆け足になりますがfromto以外で使用できる構文を列挙していきます。これらを複数同時に指定することもできます。

foreach(X,List)
リストList内の要素が順にXに設定され処理が繰り返されます。リストを生成することもできます。Xはループ内局所変数です。

foreacharg(X,StructOrArray)
StructOrArrayの部分はECLiPseのArray（[](1,2,3,4)みたいな記述)や複合項 fukugoukou(1,2,3,4) を指定します。
最初の引数から順にXに設定され処理が繰り返されます。termを生成するためには使用できません。Xはループ内局所変数です。

foreacharg(X,StructOrArray,Idx)
引数が2個のものと同じ動きですがIdxに何番目の要素がXに入っているかの数字が入ります（arg(Idx,StructOrArray,X)がtrueとなる)。XとIdxはループ内局所変数です。

foreachelem(X,Array)
foreachargと同じ動きですが2次元配列などでも対応しますArray=[]([](1,2,3),[](4,5,6))などの場合Xに1,2,3,4,5,6が順に設定される。Xはループ内局所変数です。Arrayを生成するためには使用できません。

foreachelem(X,Array,Idx)
引数2個バージョンと同じ動きですがIdxにインデックス位置が設定されます。XとIdxはループ内局所変数です。

foreachindex(Idx,Array)
foreachelemと同じ動きですがXがなくIdxのみ設定されます。Idxはループ内局所変数です。

for(I,MinExpr,MaxExpr)
C言語などのfor(I=MinExpr;I<=MaxExpr;I++)と同じ動き。MaxExprは必ず値を設定しておく必要あり。Iはループ内局所変数です。 for(I,MinExpr,MaxExpr,Increment) 引数3個バージョンと同じ動きだがIncrementで何個づつIが増えるかを設定可能 multifor(List,MinList,MaxList) for/3と同じだがIに相当する変数をリストとして複数設定する。MinListとMaxListも対応する下限上限をリストで設定する。 Listはループ内局所変数 multifor(List,MinList,MaxList,IncrementList) 引数3つバージョンと同じだがIncrementListに増加分を設定できる count(I,Min,Max) forと同じのようだがMaxは値設定しなくてOK。ループ終了後にカウントした値など把握できる。 param(Var1,Var2,...) ループ内で使用したい変数を指定する。ここで指定しない限りループの外で使用している変数など使用できない。補助述語に引数として渡すイメージ。 loop_name(Name) デバッグ用にループの名前を付けることができる。補助述語の名前のようなイメージ。他の述語と重複する名前は許されない。最後に、先ほど「fromtoなどの記述は複数記述できる」と書いたのですが、これが面白くて、例えばリストを生成する用途で使用したりなどもできます。リストList=[1,2,3,4,5]があったとして、ListSqにそれぞれの要素を2乗したリストを設定するようなプログラムを書いてみます。
```
main(LstSq):-
	Lst=[1,2,3,4,5],
	(
		fromto(Lst,[First|Rest],Rest,[]),fromto(LstSq,[FirstSq|RestSq],RestSq,[]) do
		(
			FirstSq is First*First
		)
	).
```
実行結果：
```
?- main(LstSq).
LstSq = [1, 4, 9, 16, 25]
Yes (0.00s cpu)
```
上記動作もfromtoの各引数に関して「補助述語に引数として渡している」イメージを持つと何が起こっているのかわかるのではないかと思います。

以下のような補助述語が生成されてると考えると良いと思います！
```
main(LstSq):-
	Lst=[1,2,3,4,5],
	auxiliary_predicate(Lst,LstSq).

auxiliary_predicate([],[]).
auxiliary_predicate([First|Rest],[FirstSq|RestSq]):-
	FirstSq is First*First,
	auxiliary_predicate(Rest,RestSq).
```
2021年10月28日
ECLiPSe CLPで輸送問題を解く
ECLiPSe CLPで以下の輸送問題を解きます。

問題（Problems and exercises in Operations Research 21ページ 4.5 Transportation ）：
イタリアの運送会社は、6つの店舗(Verona,Perugia,Rome,Pescara,Taranto,Lamezia)から5つの港(Genoa,Venice,Ancona,Naples,Bari)に空のコンテナを運ばなくてはならない。

6つの店舗が持っている空のコンテナの数は以下：

5つの港がそれぞれ求めているコンテナの数は以下：

コンテナはトラックで送られるが、各トラックは最大で2個のコンテナしか運べない。
また、輸送距離1kmあたり30ユーロのコストがかかる。
各店舗から各港までの距離は以下の通り：

コストが最小となるような輸送計画をもとめよ。

プログラム：
```
:- lib(eplex).
:- eplex_instance(prob). % declare an eplex instance

solve(Cost, AryL) :-
    % create the problem variables
    dim(AryC,[6,5]),	% containers
    dim(AryL,[6,5]),	% lorries
    CostConstant = [](
		[]( 290, 115, 355, 715, 810),
	    []( 380, 340, 165, 380, 610),
	    []( 505, 530, 285, 220, 450),
	    []( 655, 450, 155, 240, 315),
	    [](1010, 840, 550, 305,  95),
	    [](1072,1097, 747, 372, 333)
	  ),
	term_variables(temp(AryC,AryL), VarList),
    prob: (VarList $:: 0.0..1.0Inf),
    prob: integers(VarList),
    
    % Cost objective function(minimize this)
    (for(Row,1,6),fromto(0,RowSumIn,RowSumOut,WholeCost),param(CostConstant,AryL)
    	do
    	(
	    	for(Col,1,5),fromto(RowSumIn,ColIn,ColOut,RowSumOut),param(Row,CostConstant,AryL) do
	    	(
	    		Wk is CostConstant[Row,Col],
	    		ColOut = ColIn + Wk*AryL[Row,Col]
	    	)
    	)
   	),
   	% Empty containers constraint
    (
    	for(Row,1,6),foreach(EmptyContainer,[10,12,20,24,18,40]),param(AryC) do
    	(
    		(
	    		for(Col,1,5),fromto(0,ColIn,ColIn+AryC[Row,Col],ColCost),param(AryC,Row) do true
	    	),
	    	prob: (EmptyContainer $>= ColCost)
    	)
   	),
   	% Container demand constraint
   	(
   		for(Col,1,5),foreach(ContainerDemand,[20,15,25,33,21]),param(AryC) do
   		(
   			(
	   			for(Row,1,6),fromto(0,RowIn,RowIn+AryC[Row,Col],RowCost),param(AryC,Col) do true
	   		),
   			prob: (ContainerDemand $=< RowCost)
   		)
   	),
   	
   	% Lorries and Containers constraint 
    (
	    foreachelem(C,AryC),foreachelem(L,AryL)
	    do
	    prob:( C $=< 2*L )
	),
	
    % Set up the external solver with the objective function
    prob: eplex_solver_setup(min(30*WholeCost)),
    prob: eplex_solve(Cost), % Solve problem using external solver 
    ( foreachelem(L,AryL) 
    	do 
    	prob:eplex_var_get( L,  typed_solution, L )
    )
	.
```
実行結果：
```
?- solve(Cost, Vars).
Cost = 468510.0
Vars = []([](0, 5, 0, 0, 0), [](3, 3, 1, 0, 0), [](7, 0, 0, 3, 0), [](0, 0, 12, 0, 0), [](0, 0, 0, 1, 9), [](0, 0, 0, 13, 2))
Yes (0.02s cpu)
```
解答を整理すると以下となります。

解説：
EPLexライブラリを用いて解きました。

実は、これとほぼ同じ種類の問題がECLiPSeのTutorialにもあります（EPLexライブラリの解説の章の16.1.3 Example formulation of an MP Problem）
この問題との違いはトラック1つにつきコンテナ2つを運ぶという点だけです。

解説します。運ぶコンテナの数と実際にそれを運ぶトラックの数とを分けて考えることにします。
コンテナの数の配列をAryC、トラックの数をAryLとします。
CostConstantに輸送コストを設定しておきます(8行目)
コンテナの数、トラックの数には 0以上であること、整数であることという制約をつけます（17,18行目）
21行目からはコストの目的関数を生成してます。これを最小にするのが目標となります。この処理を抜けた段階で「WholeCost=コスト関数」の式が得られていて、これを後ほど最小化するようにEPLexに設定します(60行目)
31行目からは各店舗から送られるコンテナ数の上限が持っているコンテナ数であるという制約をつけています。
41行目からは各港に届くコンテナが要望以上であることを示す制約をつけています。
53行目からはコンテナとトラックの個数の関係の制約をつけています（各店舗-港間で移動するコンテナ数<=トラック数*2) 60行目で最適化するコスト関数を設定しています。 61行目でEPLexに問題を解くよう指示しています。 62行目からは、AryCとAryLの変数がまだEPLexの範囲用の値を持っているのを、解いた答えの値へ変更しています。
2021年10月27日
ECLiPSe でユーザー定義の算術演算子を定義する
ECLiPSe CLPでユーザー定義の算術演算子を定義して is で計算してもらえるようにする方法です。

ちなみにisで既定で計算対象となる述語はここを参照してください。

ここでは演算子の右と左の数字を直角三角形の高さと幅として、斜辺の長さを計算してくれる my_opという演算子を定義して実際に使ってます。
プログラム：
```
:- export op(200 ,yfx ,my_op).

my_op(Number1,Number2,Result):-
	Result is sqrt(Number1 * Number1 + Number2 * Number2).
```
実行結果：
```
?- A is 3 my_op 4.
A = 5.0
Yes (0.00s cpu)
```
演算子の木構造や優先度に関しては以下の記事など参考になります。
[PROLOG] compound term
[Prolog]演算子のカンマとそうでないカンマ、ドット演算子と演算子でないドット（ピリオド）

opのyfxは3つ以上数字がある場合に木構造が左に伸びてくか右に伸びてくかを決定する部分で、
例えば引き算で 6 – 2 -1 と記述した場合、
(6-2)-1 なのか
6-(2-1) なのかで答え変わってきますが、想定しているのは前者です。
このような演算子は yfxで定義します。

200の数字は演算子の優先順位です。200はECLiPSeでは+や-と同じ優先度です。小さいほど優先度が高い。ここは深く考えないでこの数字にしてしまいましたがちゃんと使う場合はまじめな検討が必要です。current_op/3という術語で演算子の優先度や結合の情報(yfxなど)が確認できます。

SWI-PROLOGでも多分同様のことできるとは思うのですが、やり方わかりませんでした。情報求ム。
2021年10月24日