ECLiPSe CLPのEPLEXライブラリを使用して混合整数線形計画問題を解きます。
混合整数計画問題とは、線形計画問題の変数のすべてもしくは一部が整数という条件がついた問題です。
Problems and exercises in Operations Research の 3.2 Gomory cutsの問題を解きます。
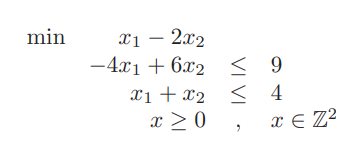
ほぼ線形計画問題と同じですが、x(x1とx2)に整数であるという条件がついています。
線形計画法の時と比べたプログラムの書き方の違いなのですがなんと整数の制約を持つ変数にintegers制約を追加するだけでできてしまいます。(下記のプログラムの13行目)
線形計画問題と混合整数計画問題の解き方の違いとして、混合整数計画問題のほうは分枝限定法を使用したり複雑な方法になるのですが、それらはライブラリの中で行ってくれるため使用する側はほとんど手間が変わりません。
プログラム:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
:- lib(eplex). :- eplex_instance(prob). % declare an eplex instance solve(Cost, Vars) :- % create the problem variables and set their range Vars = [X1,X2], prob: (Vars $:: 0.0..1.0Inf), % post the constraints for the problem to the eplex instance prob: (-4*X1 + 6*X2 $=< 9), prob: (X1 + X2 $=< 4), prob: (X1 $>= 0), prob: (X2 $>= 0), prob: integers(Vars), % set up the external solver with the objective function prob: eplex_solver_setup(min(X1 - 2*X2)), prob: eplex_solve(Cost). % Solve problem using external solver |
実行結果:
|
1 2 3 4 5 |
?- solve(Cost, [X1, X2]). Cost = -3.0 X1 = X1{0.0 .. 1.7976931348623157e+308 @ 1.0} X2 = X2{0.0 .. 1.7976931348623157e+308 @ 2.0} Yes (0.00s cpu) |
X1 = 1
X2 = 2
が解答です。かなり便利です!