ECLiPSe CLPのexampleページにあるnonogram solverを解析していて、大体理解したので説明します。(内部で regular expression constraintを使用しています。)
nonogramは日本でいうところのお絵かきロジック、ピクロスです。
ルールの説明は割愛します。
プログラムの説明も細かいところ端折ってエッセンスの説明だけします。
このプログラムの一番重要な部分は、それぞれの行列のヒントのリスト(例えば[3,3,2]など)から盤面を表すリストの制約を生成するline述語で、この内容がわかれば8割方理解したことになります。
line述語にはヒントのリストと盤面1行分(or1列分)のリストを渡します。
line述語内でfromtoを駆使してヒントからTableに怪しげなリストを生成しています。
以下の例では、tkeclipseのコンソール?で
length(Xs,15),line([3,2,3],Xs).
と入力してステップ実行した結果です。これは、ピクロスの問題でいうところの、ヒントとして「3,2,3」が与えられた15マスの1つの行の制約をつける処理に相当します。
このfromtoの説明も今回は割愛します。このプログラムではあまり良い使い方してないので他の例で学んだほうが良いです。fromtoなどのLogical Loopはかなり重要なのでいつか改めて解説記事書くと思います。
このTableなのですが、fromtoの操作が終了した時点では図のような内容になっています(右の四角内)
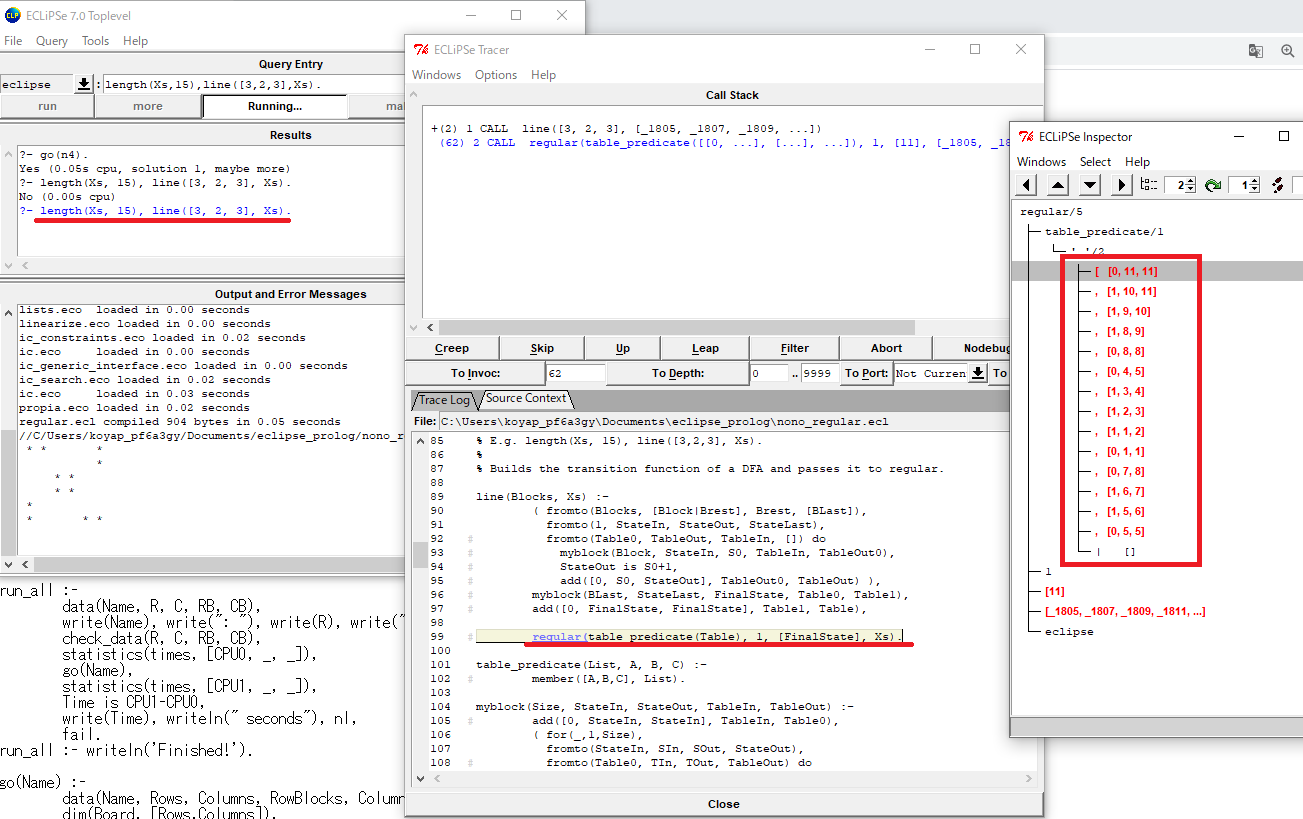
並べ替えて書くと以下の内容です(ここら辺ぐちゃぐちゃに登録してるのがこのプログラムの良くない≒テキトーなところなので見習わなくて良いです)
[0,1,1]
[1,1,2]
[1,2,3]
[1,3,4]
[0,4,5]
[0,5,5]
[1,5,6]
[1,6,7]
[0,7,8]
[0,8,8]
[1,8,9]
[1,9,10]
[1,10,11]
[0,11,11]
このリストなのですが、オートマトンの状態遷移表を意味していて、盤面のリストを左から読み込んでいった際の状態の変遷を記述してます。
3つある数字の意味は
[読み込んだ数字(0 or 1), 現在の状態, 次の状態]
を表していて、
「現在の状態 で 0または1 を読み込んだら 次はどの状態になるか」
をすべて書き出しています。
状態を11個持つ以下のようなオートマトンが出来たことになります。便宜的に状態にqをつけました。

状態はq1から開始し、矢印に書いてある数字を読み込んだ際に次の状態に遷移します。
矢印がない数字が入力された際はヒントの条件を破ってしまっているのでオートマトン不受理(エラー、制約違反)となります。
q11の状態が最終状態(受理≒読み込み終わったときにこの状態であればOK)となります。
状態遷移表が完成したのち、それをregularという術語に渡して実際の制約を作成しています。
regularの説明です。
Qsは状態のリストです。この例では15個数字を読み込むので、それぞれの読み込み時に対応したものとなります。作成したオートマトンから、上記の例だと最初の状態がq1、最後Qnがq11となります。
与えられた盤面の1行(列)のリストに「現在の状態」「次の状態」の2つの変数を追加して
[マス目の数字, 現在の状態, 次の状態]
が1要素となるリスト(この例だと要素は15個)を作成しています。
状態の部分にはQsの要素を順番に指定して以下のように隣の要素同士を関連付けています。
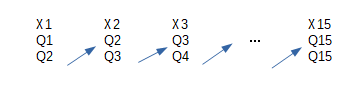
そして、それぞれの要素に関し
(Goal infers ac)@Module
で実際の制約をつけるのですが、これが実際どのようにコールされているかというと、
member([マス目の数字, 現在の状態, 次の状態], List) infers ac
という呼ばれ方です。Listの中身はオートマトンの状態遷移表です。
この操作で、[マス目の数字, 現在の状態, 次の状態]の3つの組が、オートマトンの状態遷移表の要素のいずれかの組み合わせに一致する(それ以外の組はありえない)という制約を設定しています。
member(A,L)はご存知の通り「AはL内の要素の一つ」を表すprologの組み込み述語で、ECLiPSeの制約ではありません。
ここで使用されている 「infers」というのがこのブログでも何度か触れたpropiaという仕組みで、任意のprologの述語(組み込み述語でも自作述語でも良い)をECLiPSeの制約に変換してしまうというすごい強力な仕組みです。memberは本来バックトラックを発生させてしまうため制約としては使用できないのですが、propiaを使用することにより「AはL内の要素」という意味の制約として機能するようになります。
infers ac の acの部分は制約伝搬の際にどの程度絞り込むか(候補の枝狩り)の動作に関連します。
acはarc consistency の略でアーク整合のことで、これは制約プログラミングの用語です。自分はぼんやりとしか把握してないのですがそのうちちゃんと理解したら記事書こうと思います。
infersのマニュアルページ
ちなみにECLiPSeは主にアーク整合アルゴリズムAC-3とAC-5を使用しているらしいです。
制約を作るときにオートマトンを使用するというのは面白いアイデアで今後何らかの参考になるかもしれません。
Nonogram Solverは今回解説したオートマトン使用したものの他にECLiPSeメイン開発者のJoachim Schimpfさんが作成したgecodeバージョンがあり、こちらのほうが記述が簡潔なのでそのうち解析してみたいです。