ECLiPSe CLPを用いて以下のナップサック問題を解きます。
Example の Knapsack のページ を参考にしてプログラムを作成しました。
問題（Problems and exercises in Operations Research の 18ページ 3.5 Knapsack Branch and Bound ）：
投資銀行の総予算は1400万ユーロで、4種類の投資が可能です。次の表は、投資額(Amount)と各投資による純収入(Net revenue)を示しています（単位は百万ユーロ）。投資を行う場合は、各投資を全額行う必要があります。総純収入を最大化する投資方法を答えよ。
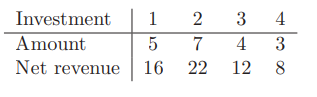
この問題文だけでは読み取れなかったのですが、解答を見ると4種類の投資は「投資しない/１個口のみ投資する」の2択らしく、同じ投資を2個以上するのは禁止のようです。
解き方：
「制約を満たす」だけではなく「利益を最大化する」「コストを最小化する」解を求める際は分枝限定法(branch_and_bound)ライブラリを使用します。
分枝限定法の厳密な定義やアルゴリズムに関しては他のページや書籍を参考にしてください。
ECLiPSe CLPのbranch and bound ライブラリでは以下の手順でコストを最小化する解を得ます。
１．コスト以外の制約を満たす解を得ます。
２．その時のコストを計算します。計算したコスト＝Aとします。
３．新たな制約「コストがA未満であること」を追加して、解を得ます。
４．上記操作を繰り返して解が得られなくなったら、直前に計算したコストが最小コストの解となります。
プログラム：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
:- lib(ic). :- lib(branch_and_bound). model(Capacity, Values, Amounts, Revenues, SumRevenues) :- ( foreach(Amount, Amounts), foreach(Value, Values), param(Capacity) do Value #::0..1 % ある投資は最大でも1回しか行えない ), integers(Amounts), sum(Amounts*Values) $= SumAmounts, SumAmounts $=< Capacity, sum(Values*Revenues) $= SumRevenues. solve(Capacity, Values, Amounts, Revenue, SumRevenues) :- model(Capacity, Values, Amounts, Revenue, SumRevenues), Cost #= -SumRevenues, minimize(search(Values, 0, largest, indomain_reverse_split, complete, []), Cost). |
解説：
6行目でValuesに[投資1,投資2,投資3,投資4]のそれぞれの投資数(0 or 1)の制約を設定しています。Valuesの個々の要素が確保されているのもこの部分ですが、動作に関してfor系の説明をしなくてはなりません。いつか改めて記事書きます。
13行目の述語solve内にある16行目の minimize/2 で分枝限定法を行っていて、繰り返し実行するgoal（この例ではsearch/6)と、コスト計算結果が入る変数（この例ではCost）を指定すると、先ほど解説した1～4の一連の動作を自動で行ってくれます。minimizeではCostを最小化する解を得ます（問題文が利益最大化を目指すものなので15行目でコスト変数への代入時に符号を逆転してます）
16行目のsearch/6の引数のうち、いくつかを説明します。
第三引数(largest): 制約変数のリストのどの変数から値を設定していくかを決める際、「一番大きい数値をドメインに持つ変数」から決定していきます（すべての変数のドメインが0 or 1なのでこのケースでは意味ないです。コピペしてきたので…）
第四引数(indomain_reverse_split) :制約変数に値を設定していくときの順番ですが、「ドメイン内の一番大きいものから降順に」値を設定していきます(このケースでは1を設定して、そのあと0を設定する）
第五引数(complete) :もれなくすべての選択肢を試します（オプションで端折るものがあります）
実行結果：
|
1 2 3 4 5 6 7 8 |
?- solve(14, Values, [5, 7, 4, 3], [16, 22, 12, 8], SumRevenues). Values = [0, 1, 1, 1] SumRevenues = 42 Yes (0.02s cpu) Found a solution with cost -38 Found a solution with cost -42 Found no solution with cost -58.0 .. -43.0 |
6行目からのFound a solution with cost ～ の部分で繰り返しコストの条件を厳しくしながらサーチしているのがわかります。
Valuesを見ると２，３，４番目の投資を行うと最大利益42を得られるようです。
上記の問題を｢0/1個口の投資」ではなく「0 ～ N個口の投資を行う」という条件に変更した際の解をサーチするプログラムもついでに掲載します。
プログラム：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
:- lib(ic). :- lib(branch_and_bound). model(Capacity, Values, Amounts, Revenues, SumRevenues) :- ( foreach(Amount, Amounts), foreach(Value, Values), param(Capacity) do % 同じ種類の投資を複数回行える条件に変更 Bound is Capacity // Amount, Value #:: 0..Bound ), integers(Amounts), sum(Amounts*Values) $= SumAmounts, SumAmounts $=< Capacity, sum(Values*Revenues) $= SumRevenues. solve(Capacity, Values, Amounts, Revenue, SumRevenues) :- model(Capacity, Values, Amounts, Revenue, SumRevenues), Cost #= -SumRevenues, minimize(search(Values, 0, largest, indomain_reverse_split, complete, []), Cost). |
7行目のところが変更部分ですが、// Amountの「//」はコメントではなくて演算子で、 「Capacity / Amount の整数部分」を計算します。
実行結果：
|
1 2 3 4 5 6 7 8 9 10 |
?- solve(14, Values, [5, 7, 4, 3], [16, 22, 12, 8], SumRevenues). Values = [2, 0, 1, 0] SumRevenues = 44 Yes (0.00s cpu) Found a solution with cost -32 Found a solution with cost -40 Found a solution with cost -42 Found a solution with cost -44 Found no solution with cost -144.0 .. -45.0 |
やはり解は変わり、44が最大利益となり、1番目の投資先に2個、3番目の投資先に1個投資するのが一番利益が高くなるようです。
ついでに、ネットで見かけた複雑そうな30個の荷物の0-1ナップサック問題を解いてみました（プログラムは前半で掲載したもの使いました）
実行結果：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
?- time(solve(499887702, Values, [137274936, 989051853, 85168425, 856699603, 611065509, 22345022, 678298936, 616908153, 28801762, 478675378, 706900574, 738510039, 135746508, 599020879, 738084616, 545330137, ...], [128990795, 575374246, 471048785, 640066776, 819841327, 704171581, 536108301, 119980848, 117241527, 325850062, 623319578, 998395208, 475707585, 863910036, 340559411, 122579234, ...], SumRevenues)). Values = [0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, ...] SumRevenues = 3673016420 Yes (0.00s cpu) Found a solution with cost -2593529208 Found a solution with cost -2967709379 Found a solution with cost -3056523353 Found a solution with cost -3188370729 Found a solution with cost -3242744021 Found a solution with cost -3243814047 Found a solution with cost -3325229604 Found a solution with cost -3326299630 Found a solution with cost -3403240143 Found a solution with cost -3535087519 Found a solution with cost -3617573102 Found a solution with cost -3671946394 Found a solution with cost -3673016420 Found no solution with cost -6192818779.0 .. -3673016421.0 Success, times: 0.000000s thread, 0.000+0.031s process, 0.036s real |
自分のマシン(Intel(R) Core(TM) i5-3340M CPU @ 2.70GHz 2.70 GHz メモリ8GB しょぼめのノートPC)では36msecで解けていました。
Example の Knapsack のページ を見ると、0/1のナップサック問題（上記の0個/1個口の投資しか許されない問題）の場合には別の解き方を行っていたり、EPLEXライブラリを使用した書き方もできることがわかります。また、ナップサック問題は分枝限定法ではなく動的計画法を用いて解くのもメジャーな解き方のようです。