ECLiPSe CLPのEPLEXライブラリを用いて線形計画法の問題を解く方法を説明します。
EPLEXは外部の数理計画法(Mathematical Programming)ソルバーで、線形計画法(Linear Programming = LP)や混合整数計画法(Mixed Integer Programming = MIP)の問題を解くことができます。
線形計画法とは複数の変数に1次方程式・1次不等式で記述されたいくつかの制約があるときに、目的関数(これも一次式)を最大化もしくは最小化する解を得るためのアルゴリズムです。
混合整数計画法は線形計画法の変数の一部もしくは全部が「整数である」という制約を持つ問題です(こっちのほうが難しいようです)
EPLEXライブラリに関してはTutorial の Chapter 16 The Eplex Libraryに使用方法が書いてあります。EPLEXはECLiPSe CLPのネイティブなライブラリではなく、外部(サードパーティ)のソルバーです。Eplexライブラリを用いることにより他のネイティブなライブラリと同じように使用可能です。また、ECLiPSe CLPをインストールした際に自動的にインストールされるので、特に設定の必要はなく初めから使えます。
世に線形計画法のソルバーはたくさんあるので、別にECLiPSe CLPを使用しなくてもよいのですが、ECLiPSeを使えば他の便利な制約論理プログラミングの制約が同時に使用できるので、のちのち良いことがあると思います。
問題は Problems and exercises in Operations Research の Chapter 2 Linear programming 2.1 Graphical solutionを解いてみます。
問題①
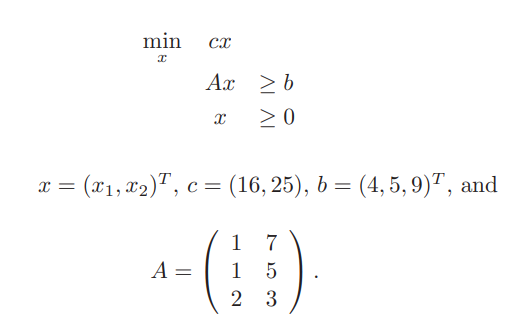
Tは転置行列です。
cx = 16*X1 + 25*X2 を最小にするような X1, X2の値を求めよという問題です。
プログラム:
:- lib(eplex). :- eplex_instance(prob). % declare an eplex instance solve(Cost, Vars) :- % create the problem variables and set their range Vars = [X1,X2], prob: (Vars $:: 0.0..1.0Inf), % post the constraints for the problem to the eplex instance prob: (1*X1+7*X2 $>= 4), prob: (1*X1+5*X2 $>= 5), prob: (2*X1+3*X2 $>= 9), prob: (X1 $>= 0), prob: (X2 $>= 0), % set up the external solver with the objective function prob: eplex_solver_setup(min(16*X1+25*X2)), prob: eplex_solve(Cost). % Solve problem using external solver
実行結果:
?- solve(Cost, [X1, X2]).
Cost = 72.142857142857139
X1 = X1{0.0 .. 1.7976931348623157e+308 @ 4.2857142857142856}
X2 = X2{0.0 .. 1.7976931348623157e+308 @ 0.14285714285714293}
Yes (0.00s cpu)
解説:
ほとんどそのまま制約を書いてあるだけですが、ポイントは
①2行目、eplex_instance()でprobという名前のインスタンスを設定し、EPLEXの機能を使うときはそのインスタンスを指定する。
②17行目、eplex_solver_setupで目的関数の設定を行う
③実行結果のX1{0.0 .. 1.7976931348623157e+308 @ 4.2857142857142856}の部分は 変数名{最小値..最大値 @ 解} の意味
くらいです。あとは見ればわかると思います。
プログラム:
:- lib(eplex). :- eplex_instance(prob). % declare an eplex instance solve(Cost, Vars) :- % create the problem variables and set their range Vars = [X1,X2], prob: (Vars $:: 0.0..1.0Inf), % post the constraints for the problem to the eplex instance prob: ( 2*X1 + X2 $=< 4), prob: (-2*X1 + X2 $=< 2), prob: ( X1 - X2 $=< 1), prob: (X1 $>= 0), prob: (X2 $>= 0), % set up the external solver with the objective function prob: eplex_solver_setup(max(3*X1+2*X2)), prob: eplex_solve(Cost). % Solve problem using external solver
実行結果:
?- solve(Cost, [X1, X2]).
Cost = 7.5
X1 = X1{0.0 .. 1.7976931348623157e+308 @ 0.5}
X2 = X2{0.0 .. 1.7976931348623157e+308 @ 3.0}
Yes (0.00s cpu)
プログラム:
:- lib(eplex). :- eplex_instance(prob). % declare an eplex instance solve(Cost, Vars) :- % create the problem variables and set their range Vars = [X1,X2,X3], prob: (Vars $:: 0.0..1.0Inf), % post the constraints for the problem to the eplex instance prob: (2*X1 + 3*X3 $=1), prob: (3*X1+2*X2 - X3 $= 5), prob: (X1 $>= 0), prob: (X2 $>= 0), prob: (X3 $>= 0), % set up the external solver with the objective function prob: eplex_solver_setup(min(X1 - 2*X2)), prob: eplex_solve(Cost). % Solve problem using external solver
実行結果:
?- solve(Cost, [X1, X2, X3]).
Cost = -5.333333333333333
X1 = X1{0.0 .. 1.7976931348623157e+308 @ 0.0}
X2 = X2{0.0 .. 1.7976931348623157e+308 @ 2.6666666666666665}
X3 = X3{0.0 .. 1.7976931348623157e+308 @ 0.33333333333333331}
Yes (0.00s cpu)
カンタンですね!
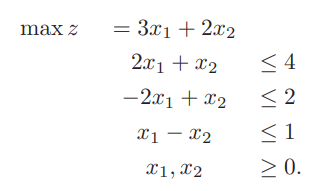
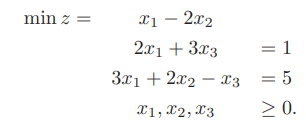
コメントを残す