ECLiPSe CLPでグラフの最短経路木を求めるやり方の紹介をします。
graph_algorithmsライブラリが使用できます。
まずmake_graph/3でグラフを作成します。引数の意味は、
第一引数:ノードの個数
第二引数:エッジ群の情報
第三引数:生成されたグラフ(戻り値)
例えば以下のグラフ(Problems and exercises in Operations Research 9ページ目 1.1 Dijkstra’s algorithm の図)の場合:
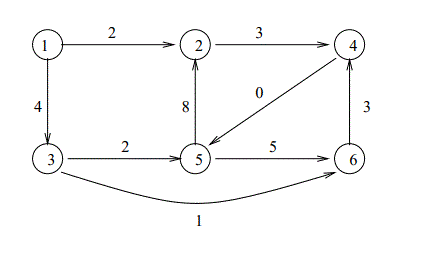
make_graph( 6, [ e(1,2,2), e(2,4,3), e(1,3,4), e(3,5,2), e(5,2,8), e(5,6,5), e(4,5,0), e(6,4,3), e(3,6,1) ], Graph)
みたいな感じで定義します。e のとこの意味は
e(ノード1番号,ノード2番号,コスト)
みたいな感じです(ノード1→ノード2の向きが存在します)
このコストのところはもっと複雑な情報を設定できるようです。
無向グラフの場合は逆向きエッジの定義も必要となります。
最短経路木なのですが、shortest_paths/4を使用して得ることが出来ます。
引数の意味は
第一引数:先ほど作ったグラフ
第二引数:e(_,_,EdgeData)で定義したエッジの3番目の引数EdgeDataのどの引数を距離(コスト)として使用するか(今回は0)
第三引数:スタート地点のノード番号
第四引数:生成された経路情報
第二引数の説明は以下を読んでください
DistanceArg refers to the graph's EdgeData information that was specified when the graph was constructed. If EdgeData is a simple number, then DistanceArg should be 0 and EdgeData will be taken as the length of the edge. If EdgeData is a compound data structure, DistanceArg should be a number between 1 and the arity of that structure and determines which argument of the EdgeData structure will be interpreted as the edge's length. Important: the distance information in EdgeData must be a non-negative number, and the numeric type (integer, float, etc) must be the same in all edges.
If DistanceArg is given as -1, then any EdgeData is ignored and the length of every edge is assumed to be equal to 1.
意訳:
DistanceArgには
・e(_,_,EdgeData)のEdgeDataが1つの数値で表されている場合は0を指定
・すべてのエッジの距離が1固定の場合は-1を指定
・「1~EdgeDataのアリティ」の範囲内で指定した場合は復号項(compound term)の何番目に距離が設定されてるかを指定したことになる
距離(コスト)は非負の数値のみ許可される。
今回の定義でノード1からすべてのノードへの最短経路を取得する場合は、以下のように呼びます
shortest_paths(Graph,0,1,Path)
プログラム全体と結果は以下のようになります。
プログラム:
:-lib(graph_algorithms). solve(Path):- make_graph( 6, [ e(1,2,2), e(2,4,3), e(1,3,4), e(3,5,2), e(5,2,8), e(5,6,5), e(4,5,0), e(6,4,3), e(3,6,1) ], Graph), shortest_paths(Graph,0,1,Path).
結果(見づらいのでPathのとこ改行しました。本当は1行でダダっと出ます):
?- solve(Path). Path = []( 0 - [], 2 - [e(1, 2, 2)], 4 - [e(1, 3, 4)], 5 - [e(2, 4, 3), e(1, 2, 2)], 5 - [e(4, 5, 0), e(2, 4, 3), e(1, 2, 2)], 5 - [e(3, 6, 1), e(1, 3, 4)] ) Yes (0.00s cpu)
結果のPathの見方なのですが、
最初の 0 – [] (おそらく自分自身へ行く経路)のあと、
ノード2へ行く最短パス、ノード3へ行く最短パス、、、ノード6へ行く最短パス
がそれぞれ表示されてます。
2 – [~]、4 – [~]の初めの数字はかかるコストが出てます。
続くリストは、どのエッジを通ったかをリストアップしてるのですが、目的地(ゴール)~ノード1(スタート)の順で出てます
以上
コメントを残す