ECLiPSe CLPで以下の輸送問題を解きます。
問題（Problems and exercises in Operations Research 21ページ 4.5 Transportation ）：
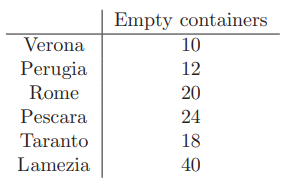
イタリアの運送会社は、6つの店舗(Verona,Perugia,Rome,Pescara,Taranto,Lamezia)から5つの港(Genoa,Venice,Ancona,Naples,Bari)に空のコンテナを運ばなくてはならない。
6つの店舗が持っている空のコンテナの数は以下：
5つの港がそれぞれ求めているコンテナの数は以下：
コンテナはトラックで送られるが、各トラックは最大で2個のコンテナしか運べない。
また、輸送距離1kmあたり30ユーロのコストがかかる。
各店舗から各港までの距離は以下の通り：
コストが最小となるような輸送計画をもとめよ。
プログラム：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
:- lib(eplex). :- eplex_instance(prob). % declare an eplex instance solve(Cost, AryL) :- % create the problem variables dim(AryC,[6,5]), % containers dim(AryL,[6,5]), % lorries CostConstant = []( []( 290, 115, 355, 715, 810), []( 380, 340, 165, 380, 610), []( 505, 530, 285, 220, 450), []( 655, 450, 155, 240, 315), [](1010, 840, 550, 305, 95), [](1072,1097, 747, 372, 333) ), term_variables(temp(AryC,AryL), VarList), prob: (VarList $:: 0.0..1.0Inf), prob: integers(VarList), % Cost objective function(minimize this) (for(Row,1,6),fromto(0,RowSumIn,RowSumOut,WholeCost),param(CostConstant,AryL) do ( for(Col,1,5),fromto(RowSumIn,ColIn,ColOut,RowSumOut),param(Row,CostConstant,AryL) do ( Wk is CostConstant[Row,Col], ColOut = ColIn + Wk*AryL[Row,Col] ) ) ), % Empty containers constraint ( for(Row,1,6),foreach(EmptyContainer,[10,12,20,24,18,40]),param(AryC) do ( ( for(Col,1,5),fromto(0,ColIn,ColIn+AryC[Row,Col],ColCost),param(AryC,Row) do true ), prob: (EmptyContainer $>= ColCost) ) ), % Container demand constraint ( for(Col,1,5),foreach(ContainerDemand,[20,15,25,33,21]),param(AryC) do ( ( for(Row,1,6),fromto(0,RowIn,RowIn+AryC[Row,Col],RowCost),param(AryC,Col) do true ), prob: (ContainerDemand $=< RowCost) ) ), % Lorries and Containers constraint ( foreachelem(C,AryC),foreachelem(L,AryL) do prob:( C $=< 2*L ) ), % Set up the external solver with the objective function prob: eplex_solver_setup(min(30*WholeCost)), prob: eplex_solve(Cost), % Solve problem using external solver ( foreachelem(L,AryL) do prob:eplex_var_get( L, typed_solution, L ) ) . |
実行結果：
|
1 2 3 4 |
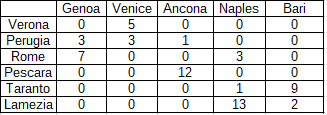
?- solve(Cost, Vars). Cost = 468510.0 Vars = []([](0, 5, 0, 0, 0), [](3, 3, 1, 0, 0), [](7, 0, 0, 3, 0), [](0, 0, 12, 0, 0), [](0, 0, 0, 1, 9), [](0, 0, 0, 13, 2)) Yes (0.02s cpu) |
解答を整理すると以下となります。
解説：
EPLexライブラリを用いて解きました。
実は、これとほぼ同じ種類の問題がECLiPSeのTutorialにもあります（EPLexライブラリの解説の章の16.1.3 Example formulation of an MP Problem）
この問題との違いはトラック1つにつきコンテナ2つを運ぶという点だけです。
解説します。運ぶコンテナの数と実際にそれを運ぶトラックの数とを分けて考えることにします。
コンテナの数の配列をAryC、トラックの数をAryLとします。
CostConstantに輸送コストを設定しておきます(8行目)
コンテナの数、トラックの数には 0以上であること、整数であることという制約をつけます（17,18行目）
21行目からはコストの目的関数を生成してます。これを最小にするのが目標となります。この処理を抜けた段階で「WholeCost=コスト関数」の式が得られていて、これを後ほど最小化するようにEPLexに設定します(60行目)
31行目からは各店舗から送られるコンテナ数の上限が持っているコンテナ数であるという制約をつけています。
41行目からは各港に届くコンテナが要望以上であることを示す制約をつけています。
53行目からはコンテナとトラックの個数の関係の制約をつけています（各店舗-港間で移動するコンテナ数<=トラック数*2)
60行目で最適化するコスト関数を設定しています。
61行目でEPLexに問題を解くよう指示しています。
62行目からは、AryCとAryLの変数がまだEPLexの範囲用の値を持っているのを、解いた答えの値へ変更しています。