ECLiPSe CLPで以下の問題を解くプログラムを書く方法を説明します。
問題(Problems and exercises in Operations Research 19ページ 4.1 Compact storage of similar sequences)
DNAマッピングプロセスの際には、非常に長い同じ長さ&ほとんど同じ並びのDNA配列をコンパクトに保存するという問題に良く遭遇する。
ここでは問題を単純化するためDNA配列を0と1の配列と仮定する。2つのビット列をそれぞれA[i]、B[i]の配列として表現したとき、これらのハミング距離は「|A[i]-B[i]|のビット列全体での総和」で定義される(= 同じ位置のビットが異なる箇所の総数)
以下の6つのビット列のそれぞれのハミング距離は以下となる(問題からコピー)

ハミング距離が大きすぎなければ、1つの完全なビット列のみストレージに記憶し、残りはそのビット列からの派生として差分のみ保存するという方法を採用できる。
上記を実現するため、全ビット列を表現するために最小の差分となるような全域木を求めよ。
解説:
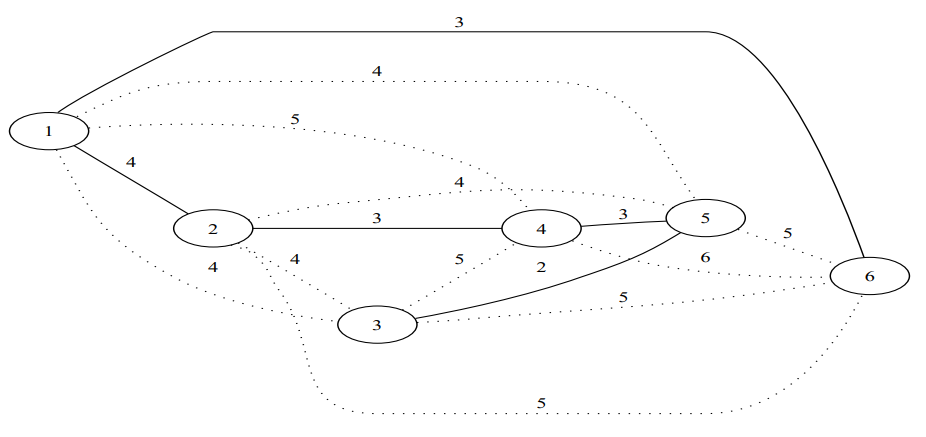
いきなりDNAとか出てきてびっくりしてしまいますが、少し考えると全ノード(ビット列)が接続されたグラフがあり、ノードを結ぶそれぞれのエッジの距離がハミング距離であるグラフを考え、その最小全域木を求める問題ということがわかります。
最小全域木を求めるためにはgraph_algorithmsライブラリ の
minimum_spanning_tree/4 という術語を使用します。
minimum_spanning_tree(+Graph, +DistanceArg, -Tree, -TreeWeight) の引数の説明
Graph:グラフ
DistanceArg:エッジ e(_,_,Distance) の Distanceの部分に数字で距離を設定する場合は0を指定
Tree:求められた最小全域木(エッジのリスト)。戻り値
TreeWeight:求められた最小全域木の総コスト。戻り値
:-lib(graph_algorithms). solve(Tree,TreeWeight):- make_graph( 6, [ e(1,2,4), e(1,3,4), e(1,4,5), e(1,5,4), e(1,6,3), e(2,3,4), e(2,4,3), e(2,5,4), e(2,6,5), e(3,4,5), e(3,5,2), e(3,6,5), e(4,5,3), e(4,6,6), e(5,6,5) ], Graph), minimum_spanning_tree(Graph, 0, Tree, TreeWeight).
実行結果
?- solve(Tree, TreeWeight). Tree = [e(3, 5, 2), e(1, 6, 3), e(2, 4, 3), e(4, 5, 3), e(1, 2, 4)] TreeWeight = 15 Yes (0.00s cpu)
コメントを残す