ECLiPSe CLPを使ってグラフの最短経路木(shortest path tree)を求める方法を説明します。
前回の例ではshortest_paths/4を使用して最短経路木を求めましたが、今回はshortest_paths_bellman_ford/4を使用しBellman-Ford’sアルゴリズムで求めます。
特徴としては、前回の例ではコストは負の数が許されなかったのですが、Bellman-Ford’sアルゴリズムでは負のコストも許されます。マニュアルには記載されていませんが前回のshortest_paths/4はおそらくダイクストラ法を使っているのではと予想しています(ソースにもコメントなし)。
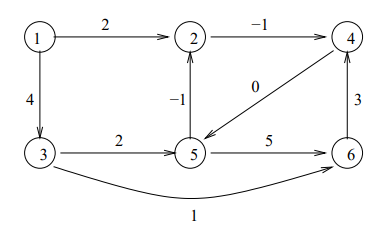
以下のようなグラフ(Problems and exercises in Operations Research 9ページ目 1.2 Bellman-Ford’s algorithm の図)で最短経路木を求めます。
shortest_paths_bellman_ford/4 の引数はコストに負数が許されること以外はshortest_paths/4と同じなので説明を割愛します(前回記事を参照)
プログラム:
:-lib(graph_algorithms). solve(Path):- make_graph( 6, [ e(1,2,2), e(2,4,-1), e(1,3,4), e(3,5,2), e(5,2,-1), e(5,6,5), e(4,5,0), e(6,4,3), e(3,6,1) ], Graph), shortest_paths(Graph,0,1,Path).
実行結果(見やすくするために改行を手で入れてます):
?- solve(Path). Path = [](0 - [], 2 - [e(1, 2, 2)], 4 - [e(1, 3, 4)], 1 - [e(2, 4, -1), e(1, 2, 2)], 1 - [e(4, 5, 0), e(2, 4, -1), e(1, 2, 2)], 5 - [e(3, 6, 1), e(1, 3, 4)]) Yes (0.00s cpu)
出力結果の見方は前回記事と同じ
総コストが負となるループがある場合(この例ではノード2->4->5) 何度もそのループを回ることでいくらでもコストを下げられるので「一番コストが低い経路」というのは存在しないのですが、ここらへんの説明はドキュメントにはありませんでした。常識的に考えるとノードを重複して通らない前提で一番コストが低い経路を返しているとは思いますが…
本記事で説明した「あるスタート地点からすべてのノードへの経路(1対N)」ではなく「あるスタート地点からあるゴールまでの経路(1対1)」を求めるsingle_pair_という接頭語が付いた述語もありますので興味のある方は調べてみてください。
コメントを残す