小屋畑ソフトウェアサービス ブログページ

カテゴリー: 制約論理プログラミング

  • DOMINO PUZZLEソルバーの解説

    ここ最近、勉強で ECLiPSe CLPのExampleページのドミノタイル問題ソルバーのソースを解析していました。大体理解したので解説したいと思います。

    問題の解説：
    0-0、0-1、0-2…..6-6 の全部で28枚のドミノタイルがある。
    tiles

    このタイルが横８×縦７の長方形の中にランダムに敷き詰められている。
    縦、横、左右逆、上下逆のどの置き方でも良い。

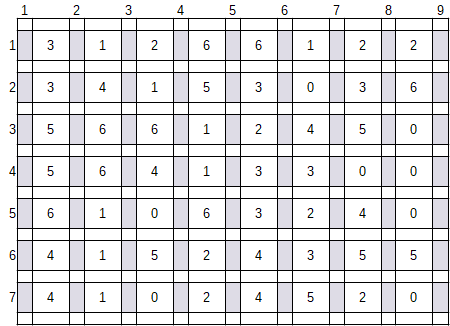
    どのように置いたかは不明で、並べた結果全体の数字が以下のようになっていた場合、タイルがどのように配置されていたかを解け。
    3 1 2 6 6 1 2 2
    3 4 1 5 3 0 3 6
    5 6 6 1 2 4 5 0
    5 6 4 1 3 3 0 0
    6 1 0 6 3 2 4 0
    4 1 5 2 4 3 5 5
    4 1 0 2 4 5 2 0

    プログラムの解説：

    プログラムの概要を説明します。
    ①述語one_by_two_tiling/4でLeftとUpというマス同士の接続状態を表す配列を作成、制約を設定します。

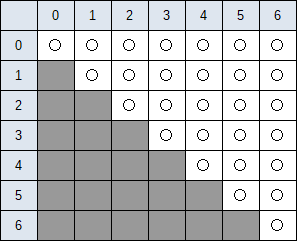
    Leftの配列は以下の色のついた部分の接続状態を表す2次元配列です。
    1つのドミノタイルとしてつながっていれば１、つながっていなければ０になります。
    lefts

    Upは以下の色のついた部分の接続状態を表す2次元配列です。
    Ups

    制約のつけ方なのですが、あるマスに注目し上下左右の接続状態を考えたとき、必ず上下左右のいずれか1つの方向のみ接続されていることになるので、そのような制約を設定します（上下左右の変数の和が１）

    ②２つのdo文で、隣接した2マスに注目しながら、「2つの数字-対応する接続変数」の組み合わせをどんどんリストに集めます。このとき、タイルは数字が小-大の順番になるようにして保存します。
    その部分にタイルが配置されていた場合は、該当する接続状態の変数が1になるというわけです。

    scan
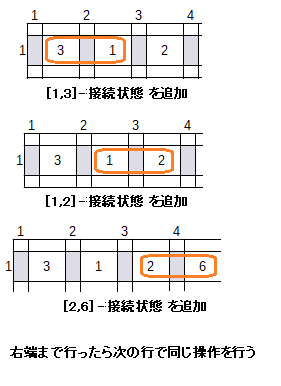
    ヨコ方向の隣接マスに注目した後は、タテ方向で同様の操作を行います。どちらも同じ配列にまとめます。
    このようにまとめると当然 (1,4)-変数 というような組み合わせが複数見つかりますが、いくつか見つかった中のどれか1つの組み合わせだけが実際に配置されているタイルの情報だということになります。

    ③まとめた配列をkeysortでソートします。タイルごとにまとまります。

    ④group_same_key_values/2で、ソート後の
    […(1,4)-接続状態変数1,(1,4)-接続状態変数2,(1,4)-接続状態変数3,(1,5)-接続状態変数4,(1,5)-接続状態変数5…]
    のような状態のリストを
    […(1,4)-[接続状態変数1,接続状態変数2,接続状態変数3],(1,5)-[接続状態変数4,接続状態変数5]…]
    のような形式にまとめます。

    ⑤
    [接続状態変数1,接続状態変数2,接続状態変数3]　の和が１
    [接続状態変数4,接続状態変数5]　の和が１
    というような制約を設定します(foreach)

    ⑥term_variableで全変数を1つのリストにまとめた後labelingですべての接続状態変数の解を探します。

    ⑦
    prety_print出力結果：
    pretty_print

  • Project Euler Problem 59

    Problem 59

    全体の文字数 – 「何文字がA-Z a-zの範囲だったか」　の数値をコストとして計算し、一番コストが小さくなるものをbb_minで調べました。
    あんまり効率よくないプログラムで、1900秒くらいかかりました…遅いな…
    あとテキストの文字数が3の倍数というところは前もって調べてて、それをあてにしたプログラムになってます（文字数が3の倍数でないとdecryptでこける）

    ソース

    :-lib(ic).
:-lib(ic_sets).
:-lib(propia).
:-lib(branch_and_bound).
:-lib(csv).

go(Str,Cost,Sum) :-
	csv:(csv_read("p059_cipher.txt", [InLst], Option)),
	char_code('a',AscA),
	char_code('z',AscZ),
	[Key1,Key2,Key3]#::AscA..AscZ,
	decrypt(InLst,OutLst,[Key1,Key2,Key3]),
	OutLst#::0..127,
	OutLst#::0..127,
	letter_count(OutLst,Cnt),
	length(OutLst,Len),
	Cost #= Len - Cnt, 
	flatten([Key1,Key2,Key3,OutLst],AllVals),
	labeling(AllVals),
	iso_light:(atom_codes(Str,OutLst)),
	mysum(OutLst,Sum).

decrypt([],[],_).
decrypt([N1,N2,N3|NRest],[D1,D2,D3|DRest],[K1,K2,K3]):-
	xor(N1,K1,D1) infers most,
	xor(N2,K2,D2) infers most,
	xor(N3,K3,D3) infers most,
	decrypt(NRest,DRest,[K1,K2,K3]).

letter_count([],0).
letter_count([First|Rest],Cnt):-
	letter_count(Rest,Cnt1),
	#::(First, [65..90, 97..122],Hit),
	Cnt #= Cnt1+Hit.

mysum([],0).
mysum([First|Rest],Sum):-
	mysum(Rest,Sum1),
	Sum is Sum1 + First.

    実行結果

    ?- bb_min(go(A, Cost, Sum), Cost, _223).
A = 復号化した文字列（伏せます）
Cost = 伏せます
Sum = 伏せます
Yes (1893.05s cpu)

  • Project Euler Problem 52

    Problem52

    ECLiPSeで解きました。
    処理時間は自分のマシン(Intel(R) Core(TM) i5-3340M CPU @ 270GHz)で6.5秒くらい。
    見どころ？はECLiPSeのlogical-loopで書いた順列permutationと、propiaで数値を入れ替えた制約を作っているところ
    logical loop はループ用のサブ述語みたいなアホっぽい定義がなくなってコードがエレガントになるのでSWI-Prologでもぜひ正式採用してほしい。
    桁のところは一般化してなく、1桁、2桁、3桁…　と手入力で増やしながら確認しました
    （bb_minでそれぞれの桁での最小の数値が取れるようにしてます）。

    プログラム：

    :-lib(ic).
:-lib(propia).
:-lib(branch_and_bound).

go(Digits,[X1num,X2num,X3num,X4num,X5num,X6num]) :-
	length(X1Lst,Digits),
	X1Lst#::[0..9],
	lst2num(X1Lst,X1num),
	X1num #> 10 ^ (Digits-1),
	X2num #= X1num * 2,
	X3num #= X1num * 3,
	X4num #= X1num * 4,
	X5num #= X1num * 5,
	X6num #= X1num * 6,
	permutation(X1Lst,X2Lst) infers most,
	lst2num(X2Lst,X2num),
	permutation(X1Lst,X3Lst) infers most,
	lst2num(X3Lst,X3num),
	permutation(X1Lst,X4Lst) infers most,
	lst2num(X4Lst,X4num),
	permutation(X1Lst,X5Lst) infers most,
	lst2num(X5Lst,X5num),
	permutation(X1Lst,X6Lst) infers most,
	lst2num(X6Lst,X6num),
	labeling([X1num,X2num,X3num,X4num,X5num,X6num]).
	
lst2num(L,N):-
	(foreach(Num,L),fromto(0,In,Out,N),count(I,0,_)
		do
		Out #= In + 10^I * Num
	).

permutation(A,B):-
	(fromto(A,AIn,AOut,[]),fromto(B,[BFirst|BRest],BRest,[])
		do
		select(BFirst,AIn,AOut)
	).

    実行結果（解答伏せます）：

    ?- bb_min(go(XXXXXXX, [N1, N2, N3, N4, N5, N6]), N1, Option).
N1 = XXXXXXXX
N2 = XXXXXXXX
N3 = XXXXXXXX
N4 = XXXXXXXX
N5 = XXXXXXXX
N6 = XXXXXXXX
Option = bb_options(continue, -1.0Inf, 1.0Inf, 1, 1, 0, 0, one, _466, _467, _468)
Yes (6.59s cpu)

  • [Prolog]最近の勉強

    最近あんまりPrologのブログ書いてませんが、ずっと研究してます(具体的にブログに書けるような結果が出てない）現在はECLiPse（IDEのほうじゃなくて制約プログラミングのほう）の勉強してます。

    書くネタないので今までのPrologの勉強の流れを説明すると以下のような感じで進んできました(スパンは数年単位）

    広井さんのページでPrologの基礎を把握しいくつかのパズルのソルバーを作る（20年近く前に大学の授業で受けていたがあまり深いところまで理解していなかった）

    ↓

    SWI-Prologのマニュアル読み込むうちCLPFDを発見し衝撃を受け、勉強開始

    ↓

    ProjectEulerでPrologで問題を解くうち、正答者スレでECLiPseを用いてSWIの自分のプログラムよりはるかに速いスピード(数十倍）で結果を出している人を発見して衝撃を受ける。プログラムの内容自体はCLPFDを使用した自分のとそんなに変わらなかった。

    ↓

    ECLiPseの勉強を始める。だんだんSWI-PrologのCLPFDがSicstusやECLiPseの制約ソルバーに比べると「オモチャ」レベルだったということがわかってくる。また、SWI-PrologのCLPFD開発者のmarkus triskaさんは開発の継続をsicstusで行うみたいな記述を最新のSWIのマニュアルで見つけた。

    また、ECLiPse は node.jsを使用してjavascriptで呼び出せるらしく、ECLiPseの勉強はWeb系の仕事でのちのち面白い威力を発揮するかもしれないと期待を抱く。

    ↓

    ECLiPseには、自分がSWIのCLPFDでどうしてもできなかった自作制約の作成がPropiaとCHRの2種類の方法で可能なことを知り、そちらの勉強を開始。SWIのCLPFDの自作制約の作成方法はマニュアルが意味不明だった（まだ完成してないとも書いてある）

    ↓

    Propiaのほうは大体の概要を把握。任意の述語をそのまま制約にできて、Propagationの厳密さをinferという述語の引数でコントロールするという仕組みらしい

    ↓

    CHRの勉強に移る。ルール自体は少ないが結構難しくてどのように作ればよいかなかなか理解できない。CHRはHaskellやJavaなどでも使用できるようだ。

    ↓

    CHRが並列計算に向いていると知り、ハードウェアで実行したりGPUを使用したりして解くといった論文をネットで見つけて読み始め、少しECLiPseの勉強から浮気する。

    ↓

    「CHRをGPUを用いて計算する｣方法を記載した論文を見つけるが実際にやった時の速度比較が載ったものを見つけることができなかったので、そういう論文が出ないかを定期的にウォッチすることに決め、とりあえず論文リサーチはやめる。CHRをハードウェアでやった論文では数万倍とかのスピードで解いてるの見つけたが良く読むとCHRの機構だけではなくプログラムのほうもハードウェア化していてちょっとちがうだろという感じだった（論文で使用している最大公約数求めるみたいな単純なロジックしかハードウェア化できなくて現実的ではないし、そもそもそれってCHR自体の速さではない）

    ↓

    またECLiPseのCHRの勉強に戻る

    △いまここです。

    まあ日本語の情報がないです。
    ずーーっと英語読んでます。ECLiPse、日本で使ってる人100人もいないんじゃなかろうか。日本のECLiPse界では望まずして第一人者になりそうです。もしそういう人たちいれば仲間に入れてほしい。誰か一緒に勉強しませんか？情報交換して一緒に研究の成果を教えあいましょう

    CHRはルール自体は3種類しかなくて単純なんだけど以下が良くわかってなくてまだ自作の制約を作るまで至ってない

    ・labelingの振る舞い
    ・制約の述語の変数に「値を設定した時？」と「新しい制約がセットされたとき？」に再度bodyがfireされるらしいがそこらへんの振る舞い

    多分CHRの制約の形が｢自分がCLPFDを勉強してきた上で持っている制約のイメージ」とかなりずれているのが理解が滞ってる理由だと思います。

    自分の数年の目標であるTantrixというパズルのソルバーをECLiPseの自作制約でいつか作れれば良いなあ。手続き型だと現在のスキルで多分作れるが制約プログラミングで作るという目標がありわざとそういう手法では作ってない

    …………………………うーん。

    この記事書いてるうちになんで自分がCHRを必死に勉強してるのか分かんなくなってきた…
    Propiaで間に合ってるような気がしてきたので、そっちでやるかな…。CHRは「つかうとすごいスピードが出るケースが見つかる(並列処理とかで）」とか「CHRで書かれためちゃくちゃエレガントなコードを見つける」みたいな状況になってから改めて勉強しようかな。
    CHRの良さをご存じの方いらっしゃればぜひ koyahata*koyahatataku.com(*を@に変更) にメール下さい。そうでなくてもProlog関連で勉強中の人はぜひ連絡取り合って一緒に勉強しましょう

    ブログまとめるのも自分の行動を見直す良い機会になりますね

    よし方向転換